বিষয়াবলী
সাধারণ ধারণা
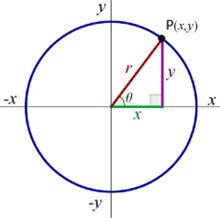
১. যে বৃত্তের কেন্দ্র মূলবিন্দু (0,0) এবং ব্যাসার্ধ r তার সমীকরণ।
x2+y2 = ry2
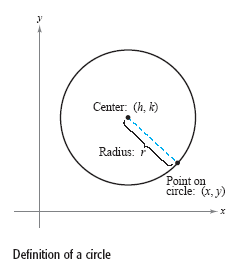
২. যে বৃত্তের কেন্দ্র (h,k) এবং ব্যাসার্ধ r তার সমীকরণ। (x-h)2+(y-k)2 = r2
h=0 হলে কেন্দ্র y অক্ষের উপর অবস্থিত। বৃত্তের সমীকরণ, x2+(y-k)2=k2
k=0 হলে কেন্দ্র x অক্ষের উপর অবস্থিত। বৃত্তের সমীকরণ, (x-h)2+y2=h2
৩. বৃত্তের সাধারণ সমীকরণ, x2+y2+2gx+2fy+c=0
যেখানে, বৃত্তের কেন্দ্র ≡ (-g,-f) এবং ব্যাসার্ধ = √(g2+f2-c)
g = 0 হলে কেন্দ্র y অক্ষের উপর অবস্থিত
f = 0 হলে কেন্দ্র x অক্ষের উপর অবস্থিত
c = 0 হলে বৃত্তটি মূলবিন্দুগামী
৪. কোনো বৃত্ত x অক্ষকে ছেদ করলে x অক্ষ থেকে কর্তিত অংশ = 2√(g2-c)
বৃ্ত্তটি x অক্ষকে স্পর্শ করলে g2=c
কোনো বৃত্ত y অক্ষকে ছেদ করলে y অক্ষ থেকে কর্তিত অংশ = 2√(f2-c)
বৃত্তটি y অক্ষকে স্পর্শ করলে f2=c
৫. কোনো বৃত্ত x অক্ষকে স্পর্শ করলে তার ব্যাসার্ধ হবে কেন্দ্রের কোটির মান এবং সমীকরণ হবে, (x-h)2+(y-k)2 = k2
৬. কোনো বৃত্ত y অক্ষকে স্পর্শ করলে তার ব্যাসার্ধ হবে কেন্দ্রের ভুজের মান এবং সমীকরণ হবে, (x-h)2+(y-k)2 = h2
৭. (x1,y1) ও (x2,y2) বিন্দু দুইটির সংযোগ সরলরেখাকে ব্যাস ধরে অঙ্কিত বৃত্তের সমীকরণ, (x-x1)(x-x2)+(y-y1)(y-y2) = 0
৮. x2+y2+2gx+2fy+c=0 বৃত্তের এককেন্দ্রিক অন্য কোনো বৃত্তের সমীকরণ হবে, x2+y2+2gx+2fy+c1=0
৯. x2+y2+2gx+2fy+c=0 বৃত্ত এবং ax+by+c1 সরলরেখার ছেদবিন্দুগামী বৃত্তের সমীকরণ, x2+y2+2gx+2fy+c+k(ax+by+c1)=0
১০. দুইটি বৃত্ত পরস্পরকে বহিঃস্থভাবে স্পর্শ করলে,
তাদের ব্যাসার্ধদ্বয়ের যোগফল = কেন্দ্রদ্বয়ের মধ্যবর্তী দূরত্ব।
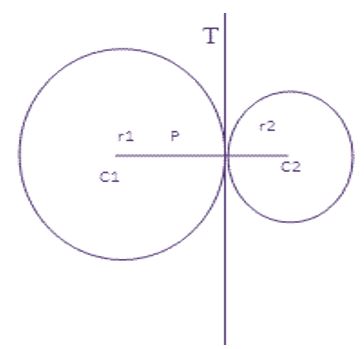
এক্ষেত্রে সাধারণ স্পর্শক তিনটি।
১১. দুইটি বৃত্ত পরস্পরকে অন্তঃস্থভাবে স্পর্শ করলে,
তাদের ব্যাসার্ধদ্বয়ের অন্তরফল = কেন্দ্রদ্বয়ের মধ্যবর্তী দূরত্ব
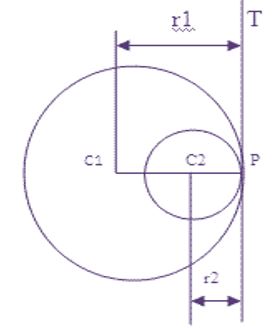
এক্ষেত্রে সাধারণ স্পর্শক একটি।
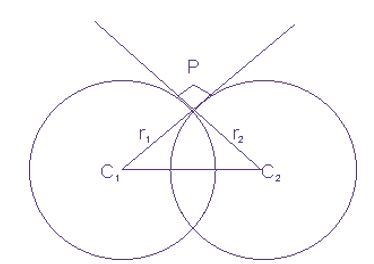
১২. দুইটি বৃত্ত পরস্পরকে ছেদ করবে যদি কেন্দ্রদ্বয়ের মধ্যবর্তী দূরত্ব ব্যাসার্ধদ্বয়ের যোগফলের থেকে ছোট হয়।
এক্ষেত্রে সাধারণ স্পর্শক দুইটি।
১৩. দুইটি বৃত্ত পরস্পরকে ছেদ বা স্পর্শ কোনোটিই করবে না যদি কেন্দ্রদ্বয়ের মধ্যবর্তী দূরত্ব ব্যাসার্ধদ্বয়ের যোগফলের চেয়ে বড় হয়।
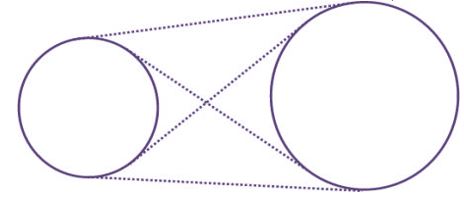
এক্ষেত্রে সাধারণ স্পর্শক চারটি।
১৪. x2+y2+2gx+2fy+c=0 এবং x2+y2+2g1x+2f1y+c1 = 0 বৃত্তের ছেদবিন্দুগামী বৃত্তের সমীকরণ, x2+y2+2gx+2fy+c+k(x2+y2+2g1x+2f1y+c1) = 0
১৫. বহিঃস্থ কোনো বিন্দু থেকে কোনো বৃত্তের ওপর দুইটি স্পর্শক অঙ্কন করা যায়।
১৬. y=mx+c সরলরেখাটি x2+y2 = r2 বৃত্তকে স্পর্শ করবে যদি,
c = ±r√(1+m2) হয়
১৭. x2+y2=r2 বৃত্তের উপরিস্থিত (x1,y1) বিন্দুতে অঙ্কিত স্পর্শকের সমীকরণ,
xx1+yy1=r2
১৮. x2+y2+2gx+2fy+c = 0 বৃত্তের (x1,y1) বিন্দুতে অঙ্কিত স্পর্শকের সমীকরণ,
xx1+yy1+g(x+x1)+f(y+y2)+c = 0
১৯. বহিঃস্থ কোন বিন্দু (x1,y1) থেকে x2+y2 = r2 বৃত্তের উপর অঙ্কিত স্পর্শকদ্বয়ের সমীকরণ, (x2+y2-r2)(x12+y12-r2)=(xx1+yy1-r2)2
২০. বহিঃস্থ বিন্দু (x1,y1) থেকে x2+y2+2gx+2fy+c=0 বৃত্তের উপর অঙ্কিত স্পর্শকদ্বয়ের সমীকরণ,
(x2+y2+2gx+2fy+c)(x12+y12+2gx1+2fy1+c) = {xx1+yy1+g(x+x1)+f(y+y1)+c}
২১. বহিঃস্থ বিন্দু (x1, y1) থেকে x2+y2=a2 বৃত্তের উপর অঙ্কিত স্পর্শকের দৈর্ঘ্য, = √(x2+y2-r2)
উক্ত বিন্দু থেকে x2+y2+2gx+2fy+c=0 বৃত্তের উপর অঙ্কিত স্পর্শকের দৈর্ঘ্য, = √(x12+y12+2gx1+2fy1+c)
২২. x2+y2 = r2 বৃত্তের (x1,y1) বিন্দুতে অভিলম্বের সমীকরণ,
x1y-y1x=0
বৃত্তের অভিলম্ব এর কেন্দ্রগামী।
২৩. x2+y2+2gx+2fy+c=0 বৃত্তের (x1,y1) বিন্দুতে অভিলম্বের সমীকরণ,
(x1+g)y-(y1+f)x+fx1-gy1=0
২৪. x2+y2+2g1x+2f1y+c1 = 0 এবং x2+y2+2g2x+2f2y+c2 = 0 বৃত্তদ্বয়ের সাধারণ জ্য এর সমীকরণ, (x2+y2+2g1x+2f1y+c1) – (x2+y2+2g2x+2f2y+c2)=0
গাণিতিক সমস্যার উদাহরণ ও সমাধান
১. 3x2+3y2-5x-6y+4=0 বৃত্তটির কেন্দ্রের স্থানাংক এবং ব্যাসার্ধ নির্ণয় কর।
সমাধানঃ
এখানে,
3x2+3y+2-5x-6y+4=0
⇒ x2+y2-(5/3)x-2y+(4/3)=0
⇒ x2+y2+2(-5/3)x+2(-1)y+(4/3)=0 ...(i)
(i) কে x2+y2+2gx+2fy+c=0 এর সাথে তুলনা করে পাই,
কেন্দ্রের স্থানাংক ≡ (-g,-f) ≡ (5/6, 1) (Ans.)
এবং ব্যাসার্ধ = √(g2+f2-c) =√(13/36) =√13/6 (Ans.)
২. (2,1), (10,1) এবং (2,-5) বিন্দু তিনটি দিয়ে অতিক্রম করে এরূপ বৃত্তের সমীকরণ নির্ণয় কর।
সমাধানঃ
ধরি, বৃত্তটির সমীকরণ, x2+y2+2gx+2fy+c=0 ...(i)
∵ বৃত্তটি (2,1) বিন্দুগামী ∴ (i) ⇒ 22+12+2.g.2+2.f.1+c=0
⇒4g+2f+c=-5 ...(ii)
∵ বৃত্তটি (10,1) বিন্দুগামী ∴ (i) ⇒102+12+2.g.10+2.f.1+c=0
⇒20g+2f+c=-101 ...(iii)
∵ বৃত্তটি (10,1) বিন্দুগামী ∴ (i) ⇒22+(-5)2+2.g.2+2f(-5)+c=0
⇒4g-10f+c=-29 ...(iv)
∴ (ii), (iii) এবং (iv) ⇒g = -6; f=2; c=15 [use calculator to solve equation]
∴ (i) ⇒ x2+y2+2(-6)x+2.2y+15=0
⇒x2+y2-12x+4y+15=0 (Ans.)
৩. (3,-10) কেন্দ্রবিশিষ্ট একটি বৃত্ত (11,-16) বিন্দু দিয়ে যায়। বৃত্তটির সমীকরণ নির্ণয় কর।
সমাধানঃ
ধরি, বৃত্তের সমীকরণ, x2+y2+2gx+2fy+c = 0 ...(i)
কেন্দ্রের স্থানাংক ≡ (3,-10)
∴ g = -3; f=10
∴ (i) ⇒x2+y2-6x+20y+c = 0 ...(ii)
∵ বৃত্তটি (11, -16) বিন্দুগামী
∴(ii) ⇒112+(-16)-6(11)+20(-16)+c=0
⇒c=9
∴ (ii) ⇒x2+y2-6x+20y+9=0 (Ans.)
অথবা,
∵ বৃত্তের কেন্দ্র (3,-10) এবং বৃত্তটি (11,-16) বিন্দু দিয়ে যায়
∴ বৃত্তের ব্যাসার্ধ = (3,-10) ও (11,-16) বিন্দুদ্বয়ের মধ্যবর্তী দূরত্ব
= √{(3-11)2+(-10+26)2}
[(x1,y1) ও (x2,y2) বিন্দুদ্বয়ের মধ্যবর্তী দূরত্ব = √{(x1-x2)2+(y1-y2)2 }]
= √100
∴(3,-10) কেন্দ্রবিশিষ্ট √100 ব্যাসার্ধের বৃত্তের সমীকরণ,
(x-3)2+(y+10)2 = 100 [(h,k) কেন্দ্রবিশিষ্ট r ব্যাসার্ধের বৃত্তের সমীকরণ, (x-h)2+(y-k)2 = r2]
শর্টকাট: (x1,y1) কেন্দ্রবিশিষ্ট (x2,y2) বিন্দুগামী বৃত্তের সমীকরণ।
(x-x1)2+(y-y1)2 = (x1-x2)+(y1-y2)2
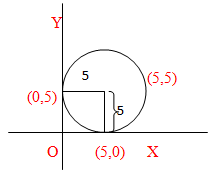
৪. এমন একটি বৃত্তের সমীকরণ নির্ণয় কর যা প্রত্যেক অক্ষরেখাকে মূলবিন্দু থেকে ধনাত্মক দিকে 5 একক দূরত্বে স্পর্শ করে।
সমাধানঃ
এখানে, বৃত্তটি x অক্ষকে (5,0) এবং y অক্ষকে (0,5) বিন্দুতে স্পর্শ করে।
∴ কেন্দ্রের ভুজ = 5 ; কোটি = 5 ; স্থানাংক ≡ (5,5) এবং ব্যাসার্ধ = x অক্ষ থেকে কেন্দ্রের দূরত্ব = y অক্ষ থেকে কেন্দ্রের দূরত্ব = 5
∴ বৃত্তের সমীকরণ, (x-5)2+(y-5)2 = 25
⇒x2+y2-10x-10y+25 = 0
৫. একটি বৃত্ত y অক্ষকে মূলবিন্দুতে স্পর্শ করে এবং (3,-4) বিন্দু দিয়ে যায়। বৃত্তটির সমীকরণ নির্ণয় কর।
সমাধানঃ
ধরি, বৃত্তটির সমীকরণ, x2+y2+2gx+2fy+c=0 ...(i)
∵ বৃত্তটি মূলবিন্দু দিয়ে যায় ∴c = 0
∵ বৃত্তটি অক্ষকে স্পর্শ করে ∴f2 = c = 0
∴ (i)⇒x2+y2+2gx=0 ...(ii)
∵ বৃত্তটি (3,-4) বিন্দুগামী ∴ (ii)⇒32+(-4)2+2g(3)=0
⇒ g = -(25/6)
∴ বৃত্তটির সমীকরণ (ii)⇒x2+y2+2(-25/6)x = 0
⇒3x2+3y2-25x = 0
৬. এরূপ বৃত্তের সমীকরণ নির্ণয় কর যা x অক্ষকে (4,0) বিন্দুতে স্পর্শ করে এবং y অক্ষ থেকে 6 একক দৈর্ঘ্য বিশিষ্ট জ্যা খণ্ডিত করে।
সমাধানঃ
ধরি, বৃত্তের সমীকরণ, x2+y2+2gx+2fy+c=0 ...(i)
∵ বৃত্তটি x অক্ষকে (4,0) বিন্দুতে স্পর্শ করে ∴ কেন্দ্রের ভুজ = 4=-g এবং g2 = c
⇒c=16
∵ বৃত্তটি y অক্ষ থেকে 6 একক অংশ ছেদ করে, ∴ 2√(f2-c) = 6
⇒f2-c = 9
⇒f2 = 25
⇒f = ±5
∴ (i)⇒x2+y2+2(-4)x+2(±5)y+16=0
⇒x2+y2-8x±10y+16=0 (Ans.)
৭. একটি বৃত্ত (3,5) ও (6,4) বিন্দু দিয়ে অতিক্রম করে এবং এর কেন্দ্র (i) x+2y-10=0 রেখার উপর অবস্থিত (ii) x অক্ষের উপর অবস্থিত (iii) y অক্ষের উপর অবস্থিত। i বৃত্তটির সমীকরণ নির্ণয় কর।
সমাধানঃ
ধরি, বৃত্তের সমীকরণ, x2+y2+2gx+2fy+c=0 ...(i)
∵বৃত্তটি (3,5) বিন্দুগামী ∴ (i)⇒(3)2+(5)2+2(3)g+2(5)f+c=0
⇒6g+10f+c=-34 ...(ii)
∵ বৃত্তটি (6,4) বিন্দুগামী ∴ (i)⇒(6)2+(4)2+2(6)g+2(4)f+c=0
⇒12g+8f+c=-52 ...(ii)
(i)
বৃত্তের কেন্দ্রের স্থানাংক ≡ (-g,-f)
কিন্তু কেন্দ্র x+2y-10=0 রেখার উপর অবস্থিত।
∴ -g+2(-f)-10=0
⇒g+2f=-10 ...(iv)
∴ (ii), (iii) ও (iv)⇒g=-4; f=-3; c=20
∴ (i)⇒x2+y2+2(-4)x+2(-3)y+20=0
⇒x2+y2-8x-6y+20=0 (Ans.)
(ii)
কেন্দ্র x অক্ষের উপর অবস্থিত হলে কেন্দ্রের কোটি =-f=0
∴ (ii)⇒6g+c=-34
এবং (iii)⇒12g+c=-32
∴ g=-3; c=-16
∴ (i)⇒x2+y2+2(-3)x+2(0)y-16=0
⇒x2+y2-6x-16=0 (Ans.)
(iii)
কেন্দ্র y অক্ষের উপর অবস্থিত হলে কেন্দ্রের ভুজ =-g=0
∴(ii)⇒10f+c=-34 এবং (iii)⇒8f+c=-52
∴ f=9; c=-124
∴ (i)⇒x2+y2+2(0)x+2(9)y-124=0
⇒x2+y2+18y-124=0 (Ans.)
৮. x2+y2-3x+10y=15=0 বৃত্তের (4,-11) বিন্দুতে স্পর্শকের সমীকরণ নির্ণয় কর।
এখানে, x2+y2-3x+10y=15=0
⇒x2+y2+2(-3/2)x+2.5.y-15=0
∴ নির্ণেয় সমীকরণ, x.4+y(-11)-(3/2)(x+4)+5(y-11)-15=0
⇒5x-12y-152=0 (Ans.)
৯. x2+y2=b(5x-12y) বৃত্তে অঙ্কিত ব্যাস মূলবিন্দু দিয়ে যায়। এই ব্যাসের সমীকরণ এবং মূলবিন্দুতে অঙ্কিত স্পর্শকটির সমীকরণ নির্ণয় কর।
সমাধানঃ
এখানে, x2+y2 = b(5x-12y)
⇒x2+y2-5bx+12by=0
⇒ x2+y2+2(-5b/2)x+2(6b)y=0
∴ কেন্দ্রের স্থানাংক ≡ (-g,-f) = (5b/2, -6b)
∴ মূলবিন্দু দিয়ে অতিক্রান্ত ব্যাসের সমীকরণ হবে মূলবিন্দু (0,0) এবং কেন্দ্রের (5b/2, -6b) সংযোগকারী রেখা,
$\frac{y}{-6 b}=\frac{x}{\frac{5 b}{2}}$ [(0,0) এবং (x2,y2) বিন্দুদ্বয়ের সংযোগকারী রেখার সমীকরণ y/y1=x/x1]
⇒y=-(12/5)x
⇒12x+5y=0 (Ans.)
∴ মূলবিন্দুতে অঙ্কিত স্পর্শক উক্ত ব্যাসের উপর লম্ব হবে।
∴ স্পর্শকের সমীকরণ, 5x-12y=0 [ax+by=0 রেখার লম্ব রেখার সমীকরণ, bx-ay=0]
১০. মূলবিন্দু থেকে (1,2) কেন্দ্রবিশিষ্ট বৃত্তের উপর অঙ্কিত স্পর্শকের দৈর্ঘ্য 2 একক। বৃত্তটির সমীকরণ নির্ণয় কর।
সমাধানঃ
ধরি, বৃত্তটির সমীকরণ, x2+y2+2gx+2fy+c=0 ...(i)
কেন্দ্রের স্থানাংক ≡ (-g,-f)=(1,2)
∴ g = -1 ; f = -2
∴ (i) ⇒x2+y2-2x-4y+c=0 ...(ii)
মূলবিন্দু থেকে উক্ত বৃত্তের উপর অঙ্কিত স্পর্শকের দৈর্ঘ্য
⇒√{02+02-2(0)-4(0)+c}=2 [(x1,y1) বিন্দু থেকে x2+y2+2gx+2hy+c=0 বৃত্তে অঙ্কিত স্পর্শকের দৈর্ঘ্য = (x2+√y2+2gx+2hy+c)]
⇒ c = 4
∴ (ii) ⇒ x2+y2-2x-4y+4=0 (Ans.)
১১. x2+y2-4x+6y-36=0 এবং x2+y2-5x+8y-43=0 বৃত্ত দুইটির সাধারণ জ্যা এর সমীকরণ নির্ণয় কর।
সমাধানঃ
নির্ণেয় সমীকরণ, x2+y2-4x+6y-36-(x2+y2-5x+8y-43)=0
⇒x2+y2-4x+6y-36-x2-y2+5x-8y+43=0
⇒x-2y+7=0 (Ans.)
শর্টকাট: এক্ষেত্রে সাধারণ স্পর্শকের সমীকরণ, (2g1-2g2)x+(2f1-2f2)y+(c1-c2)=0
