বিষয়াবলী
সাধারণ ধারণা
কণিক : কার্তেসীয় সমতলে একটি নির্দিষ্ট বিন্দু ও একটি নির্দিষ্ট সরলরেখা থেকে যে সব বিন্দুর দূরত্বের অনুপাত একটি ধ্রুবক, তাদের সেই একটি সঞ্চারপথ এবং তাকে কণিক বলা হয় ।
- নির্দিষ্ট বিন্দুটিকে কণিকের উপকেন্দ্র বা ফোকাস (focus) বলে।
- নির্দিষ্ট সরলরেখাটিকে কণিকের দিকাক্ষ বা নিয়ামক (directrix) বলে ।
- ধ্রুব অনুপাতটিকে উৎকেন্দ্রিকতা (eccentricity) বলা হয় এবং দ্বারা e সূচিত করা হয় ।
- e এর বিভিন্ন মানের জন্য সঞ্চারপথের আকৃতি ভিন্ন হয় ।
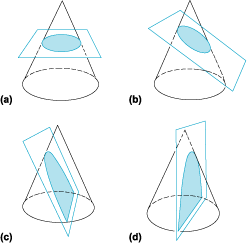
- e = 0 হলে সঞ্চারপথ হয় বৃত্ত (circle)
- 0 < e < 1 হলে সঞ্চারপথ হয় উপবৃত্ত (ellipse)
- e = 1 হলে সঞ্চারপথ হয় পরাবৃত্ত (parabola)
- e > 1 হলে সঞ্চারপথ হয় অধিবৃত্ত (hyperbola)
- পরাবৃত্ত (Parabola) সম্পর্কিত কিছু সংজ্ঞা:
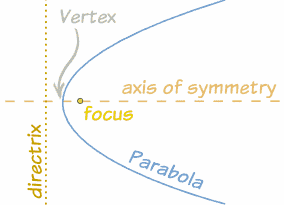
অক্ষরেখা (Axis of symmetry): উপকেন্দ্রের মধ্য দিয়ে দিকাক্ষের উপর অঙ্কিত লম্ব রেখাটিকে পরাবৃত্তের অক্ষরেখা বলা হয়।
শীর্ষবিন্দু (Vertex): পরাবৃত্ত ও অক্ষরেখার ছেদ বিন্দুকে পরাবৃত্তের শীর্ষবিন্দু বলা হয়।
উপকেন্দ্রিক দূরত্ব (Focal distance): উপকেন্দ্র থেকে পরাবৃত্তের যেকোনো বিন্দুর দূরত্বকে উপকেন্দ্রিক দূরত্ব বা ফোকাস দূরত্ব বলা হয়।
উপকেন্দ্রিক জ্যা (Focal chord): পরাবৃত্তের যে জ্যা উপকেন্দ্র দিয়ে গমন করে তাকে উপকেন্দ্রিক জ্যা বলে।
উপকেন্দ্রিক লম্ব (Latus rectum): উপকেন্দ্রিক জ্যা অক্ষের উপর লম্ব হলে তাকে উপকেন্দ্রিক লম্ব বা নাভিলম্ব বলে।
- y2 = 4ax পরাবৃত্তের ক্ষেত্রে :
- শীর্ষবিন্দু, (0,0)
- উপকেন্দ্র, (a,0)
- দিকাক্ষের সমীকরণ, x = -a
- অক্ষরেখার সমীকরণ, y = 0
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য, = 4a
- উপকেন্দ্রিক লম্বের সমীকরণ, x = a
- y2 = -4ax পরাবৃত্তের ক্ষেত্রে :
- (0,0)
- (-a,0)
- x = a
- y = 0
- 4a
- x = -a
- x2 = -4ay পরাবৃত্তের ক্ষেত্রে :
- (0,0)
- (0,a)
- y = -a
- x = 0
- 4a
- y = a
- x2 = -4ay পরাবৃত্তের ক্ষেত্রে :
- (0,0)
- (0,-a)
- y = a
- x = 0
- 4a
- y = -a
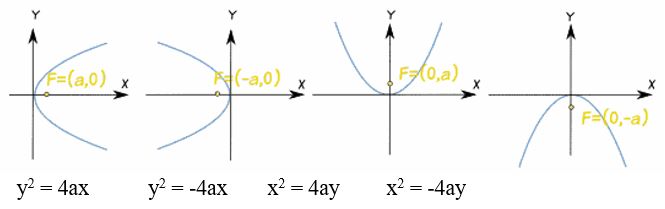
উপবৃত্ত (Ellipse)
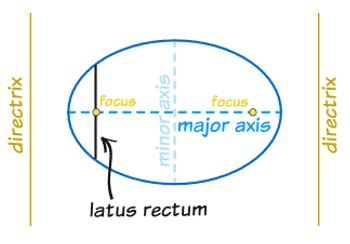
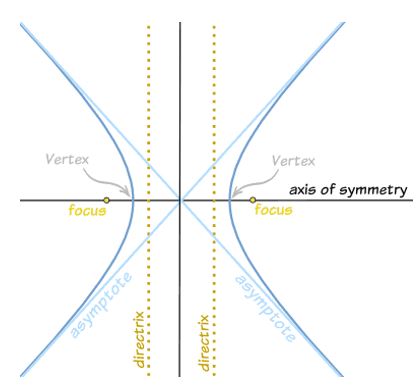
অধিবৃত্ত (hyperbola)
-
- x2/a2 + y2/b2 = 1 উপবৃত্তের ক্ষেত্রে : (যখন a>b)
- কেন্দ্রের স্থানাংক (0,0)
- বৃহৎ অক্ষ (major axis) = 2a
- ক্ষুদ্র অক্ষ (minor axis) = 2b
- উপকেন্দ্রের সমীকরণ (±ae,0)
- বৃহৎ অক্ষের সমীকরণ, y = 0
- ক্ষুদ্র অক্ষের সমীকরণ, x = 0
- দিকাক্ষের সমীকরণ, x = ± (a/e)
- উৎকেন্দ্রিকতা, e2 = (a2-b2) / a2
- উপকেন্দ্রিক লম্ব = 2b2 / a
- x2/a2 + y2/b2 = 1 উপবৃত্তের ক্ষেত্রে : (যখনa<b)
- (0,0)
- 2b
- 2a
- (0,±b e)
- x = 0
- y = 0
- y = ± (b/ e)
- e2 = (b2-a2) / b2
-
- x2/a2 - y2/b2 = 1 অধিবৃত্তের ক্ষেত্রে :
- কেন্দ্রের স্থানাংক (0,0)
- উপকেন্দ্রদ্বয়ের স্থানাংক (e,0)
- শীর্ষবিন্দুর স্থানাংক (±a,0)
- দিকাক্ষের সমীকরণ, x = ±(a/e)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য = 2b2/a
- উপকেন্দ্রিক লম্বের সমীকরণ, x = ±ae
- উৎকেন্দ্রিকতা, e2 = (a2+b2) / a2
- আড় অক্ষের সমীকরণ, y = 0
- অনুবন্ধী অক্ষের সমীকরণ, x = 0
- আড় অক্ষের দৈর্ঘ্য = 2a
- অনুবন্ধী অক্ষের দৈর্ঘ্য = 2b
- y2/b2 - x2/a2 = 1 অধিবৃত্তের ক্ষেত্রে :
- (0,0)
- (0,±be)
- (0,±b)
- y = ±(b/e)
- 2b2/a
- y = ±be
- e2 = (b2+a2)/b2
- x = 0
- y = 0
- 2b
- 2a
গাণিতিক সমস্যা ও সমাধান
1. 5x2 + 15x – 10y – 4 = 0 পরাবৃত্তের শীর্ষবিন্দু, উপকেন্দ্র, উপকেন্দ্রিক লম্ব, অক্ষরেখা এবং দিকাক্ষের সমীকরণ নির্ণয় কর ।
সমাধান:
এখানে, 5x2 + 15x – 10y – 4 = 0
⇒ 5(x2+3x) – 10y – 4 = 0
⇒ 5 (x2 + 2.x.3/2 + 9/4) – 5.9/4 – 10y – 4 = 0
⇒ 5 (x + 3/2 )2 = 10y + 61/4
⇒ (x + 3/2)2 = 2 (y + 61/40) ...(i)
ধরি, x + 3/2 = X এবং y + 61/40 = Y
∴ (i) ⇒ x2 = 2y ⇒ x2 = 4 . 1/2 . y
x2 = 4ay পরাবৃত্তের সমীকরণের সাথে তুলনা করে পাই,
শীর্ষবিন্দুর ভুজ, x = 0 ⇒ x + 3/2 = 0 ⇒ x = - 3/2
শীর্ষবিন্দুর কোটি, y = 0 ⇒ y + 61/40 = 0 ⇒ y = - 61/40
∴ শীর্ষবিন্দুর স্থানাংক ≡ (-3/2, -61/40) [ans.]
উপকেন্দ্রের ভুজ, x = 0 ⇒ x + 3/2 = 0 ⇒ x = -3/2
উপকেন্দ্রের কোটি,y = a = ½
⇒ y + 61/40 = ½ ⇒ y = -41/40
∴ উপকেন্দ্রের স্থানাংক ≡ (-3/2, - 41/40) [ans.]
অক্ষরেখার সমীকরণ, x = 0 ⇒ x + 3/2 = 0 [ans.]
দিকাক্ষের সমীকরণ, y = -a = -1/2
⇒ y + 61/40 + ½ = 0 ⇒ y + 81/40 = 0 [ans.]
2. (1,1) উপকেন্দ্র ও 3x+4y = 1 দিকাক্ষবিশিষ্ট পরাবৃত্তের সমীকরণ নির্ণয় কর । তার অক্ষের সমীকরণও বের কর ।
সমাধান:
ধরি, P (x,y) পরাবৃত্তের উপরিস্থিত কোনো বিন্দু । P থেকে উপকেন্দ্রের দূরত্ব PS এবং দিকাক্ষের লম্ব দূরত্ব PM হলে,
PS = ePM
⇒ PS = PM [পরাবৃত্তের জন্য e=1]
$\Rightarrow \sqrt{(x-1)^{2}+(y-1)^{2}}=\frac{|3 x+4 y-1|}{\sqrt{3^{2}+4^{2}}}$
[(x1,y1) ও (x2,y2) বিন্দুদ্বয়ের মধ্যবর্তী দূরত্ব = $\sqrt{\left(\mathrm{x}_{1}-\mathrm{x}_{2}\right)^{2}+\left(\mathrm{y}_{1}-\mathrm{y}_{2}\right)^{2}}$ ; (x1,y1) থেকে
ax+by+c = 0সরলরেখার দূরত্ব = $\frac{\left|\mathrm{ax}_{1}+\mathrm{by}_{1}+\mathrm{c}\right|}{\sqrt{\mathrm{a}^{2}+\mathrm{b}^{2}}}$ ]
⇒ (x-1)2 + (y-1) = (3x+4y-1)2 / 32+42
⇒ 25x2+ 25y2-50x-50y+50 = 9x2+16y2+1+24xy-8y-6x
⇒ 16x2+9y2-44x-42y+49-24xy = 0
⇒ (4x-3y)2-44x-42y+49 = 0 [Answer]
অক্ষ দিকাক্ষের উপর উপর লম্ব । তাই অক্ষের সমীকরণ হবে,
4x-3y+k = 0 [ax+by+c = 0 রেখার লম্ব রেখার সমীকরণ, bx-ay+k = 0]
∵ অক্ষ (1,1) বিন্দুগামী,
∴ 4(1)-3(1)+k = 0
⇒ k = -1
∴ অক্ষের সমীকরণ, 4x-3y-1 = 0
[ans.]
3. 16x2+25y2 = 400 উপবৃত্তের উৎকেন্দ্রিকতা, উপকেন্দ্র, উপকেন্দ্রিক লম্বের দৈর্ঘ্য এবং উপকেন্দ্রিক লম্ব ও দিকাক্ষের সমীকরণ নির্ণয় কর ।
সমাধান:
এখানে, 16x2+25y2 = 400
⇒ x2/25 + y2/16 = 1
∴ a = 5 এবং b = 4
∵ a>b ∴ e2 = (a2-b2)/a2 = 9/25
⇒ e = 3/5 [e ঋণাত্মক হতে পারে না] [ans.]
উপকেন্দ্রের স্থানাংক ≡ (±e,0) = (±3,0)
উপকেন্দ্রিক লম্বের দৈর্ঘ্য = 2b2/a = 32/5 [ans.]
উপকেন্দ্রিক লম্বের সমীকরণ, x = ±e ⇒ x = ±3 [ans.]
দিকাক্ষের সমীকরণ, x = (±a/e) ⇒ x = ± 25/3 [ans.]
4. x2-3y2-2x = 8 অধিবৃত্তের উৎকেন্দ্রিকতা, কেন্দ্রের স্থানাংক এবং অক্ষের দৈর্ঘ্য নির্ণয় কর ।
সমাধান:
এখানে, x2-3y2-2x = 8
⇒ (x2-2x.1+1)-3y2 = 8+1
⇒ (x-1)2-3y2 = 9
⇒ (x-1)2 / 9 – y2/3 = 1
∴ a2 = 9 ; b2 = 3
∴ 2 = (a2+b2) / a2 = 4/3
∴ e = 2/√3 [ans.]
কেন্দ্রের ভুজ, x-1 = 0 ⇒ x = 1
কেন্দ্রের কোটি, y = 0
∴ কেন্দ্রের স্থানাংক ≡ (1,0) [ans.]
আড় অক্ষের দৈর্ঘ্য = 2a = 6 [ans.]
অনুবন্ধী অক্ষের দৈর্ঘ্য = 2b = 2√3 [ans.]
