উত্তর ভুল মনে হলে নিচে মন্তব্য করুন
পদার্থবিজ্ঞান
১. স্থির অবস্থায় থাকা একটি বস্তু বিস্ফোরণের ফলে M1 এবং M2 ভরের দুটি খণ্ডে বিভক্ত হয় এবং খণ্ড দুটি বিপরীত দিকে যথাক্রমে V1 এবং V2 বেগ প্রাপ্ত হয়। V1 এবং V2 এর অনুপাত কত?
ক. M1 / M2
খ. M2 / M1
গ. (M1 / M2)1/2
ঘ. (M1 / M2)1/2
উত্তর : খ. M2 / M1
সামাধান :
এখানে, M1V1 = M2V2, ∴ V2 / V1 = M2 / M1
২. একটি ঘরের বিপরীত দু’দেয়ালের মধ্যবর্তী দূরত্ব 4 m, একটি দেয়ালে একটি অবতল দর্পণ লাগানো আছে। দর্পণ হতে 2.5 m দূরে একটি বস্তু রাখলে তার প্রতিবিম্ব বিপরীত দেয়ালে গঠিত হয়। দর্পণের ফোকাস দূরত্ব কত?
ক. 2.5 m
খ. 1.54 m
গ. 1.44 m
ঘ. 2.25 m
উত্তর : খ. 1.54 m
সামাধান :
 $\frac{1}{u}+\frac{1}{v}=\frac{1}{f}, \therefore \mathrm{f}=\frac{u v}{u+v}=\frac{4 x 2.5}{4+2.5}=1.54$
$\frac{1}{u}+\frac{1}{v}=\frac{1}{f}, \therefore \mathrm{f}=\frac{u v}{u+v}=\frac{4 x 2.5}{4+2.5}=1.54$
৩. একটি তেজস্ক্রিয় পদার্থের অর্ধায়ু 1600 বছর। কত সময় পরে তেজস্ক্রিয় পদার্থের 15/16 অংশ ক্ষয়প্রাপ্ত হবে?
ক. 1500 years
খ. 4800 years
গ. 6400 years
ঘ. 9600 years
উত্তর : গ. 6400 years
সামাধান :
$\mathrm{t}_{1 / 2}=1600$ বছর,
$\therefore \lambda=\frac{0.693}{1600}$
এখন, $\mathrm{N}=\mathrm{N}_{0} \mathrm{e}^{-\lambda \mathrm{t}}$ ,
এখানে $\mathrm{N}=(1 / 16) \times \mathrm{N}_{0}, \therefore \mathrm{t}=-\frac{\ln \frac{1}{16}}{(0.693 / 1600)}=6400$ বছর
৪. Higgs প্রক্রিয়া এক ধরনের -
ক. ভর তৈরির প্রক্রিয়া
খ. শক্তি তৈরির প্রক্রিয়া
গ. ইলেকট্রন তৈরির প্রক্রিয়া
ঘ. বল তৈরির প্রক্রিয়া
উত্তর : ক. ভর তৈরির প্রক্রিয়া
সূত্র : Wikipedia
৫. নিম্নের কোন ভৌত প্রক্রিয়া শব্দ তরঙ্গ দ্বারা প্রদর্শিত হয় না?
ক. প্রতিসরণ
খ. ব্যতিচার
গ. সমবর্তন
ঘ. অপবর্তন
উত্তর : গ. সমবর্তন
সূত্র : Wikipedia
৬. পৃথিবীপৃষ্ঠে মহাকর্ষীয় প্রাবল্য g, কাল্পনিক একটি গ্রহের ঘনত্ব যদি পৃথিবীর ঘনত্বের সমান হয় এবং ব্যাসার্ধ যদি দ্বিপুণ হয় তবে এই গ্রহের পৃষ্ঠে মহাকর্ষীয় ক্ষেত্র প্রাবল্য কত?
ক. g
খ. 2g
গ. 4g
ঘ. 8g
উত্তর : 2g
সামাধান :
$g_{\text {earth }}=\frac{G M}{R^{2}}=\frac{G \rho\left(4 \pi R^{3}\right)}{R^{2}}=G \rho 4 \pi R, \therefore g_{\text {planet }}=G \rho 4 \pi(2 R)=2 \times g_{\text {earth }}$
৭. একটি বৈদ্যুতিক ইস্ত্রিতে 220 V এবং 1200 W লেখা আছে। যদি প্রতি ইউনিট বিদ্যুৎ শক্তির মূল্য 1.00 টাকা হয়, তাহলে ইস্ত্রিটি 2 ঘণ্টা চালালে কত খরচ পড়বে?
ক. 3 টাকা
খ. 2.6 টাকা
গ. 2.3 টাকা
ঘ. 2.4 টাকা
উত্তর : ঘ. 2.4 টাকা
সামাধান :
P = 1200 W, t = 2 hour, ∴ খরচ = (Pt/1000) x 1.00 = 2.4 টাকা
৮. নিচের লেখচিত্রে 50 s সময়কালে একটি গাড়ির বেগের পরিবর্তন দেখানো হয়েছে। এই সময়কালে গাড়িটি কত দূরত্ব অতিক্রম করেছে?
ক. 500 m
খ. 400 m
গ. 350 m
ঘ. 300 m
উত্তর : গ. 350 m
সামাধান :
প্রথম ২০ সেকেন্ডে ১০০ অতিক্রম করে। $\mathrm{S}=\frac{(0+v)}{2} x t=5 \times 20=100$
পরবর্তী ২০ সেকেন্ডে s = vt = 200
শেষ ১০ সেকেন্ডে $\mathrm{S}=\frac{(0+v)}{2} x t=5 \times 20=100$, ∴ মোট = 350 m
৯. 0°C তাপমাত্রার 2.1 kg বরফ 40°C তাপমাত্রার 5.9 kg পানির সাথে মিশ্রিত করা হলো। মিশ্রণের তাপমাত্রা কত হবে? পানির আপেক্ষিক তাপ = 4.2x103 J Kg-1 K-1, বরফ গলনের আপেক্ষিক সুপ্ততাপ = 3.36x105 J Kg-1 K-1
ক. 7.5°C
খ. 9.5°C
গ. 10.5°C
ঘ. 8.5°C
উত্তর : ঘ. 8.5°C
সামাধান :
$2.21 \times 3.36 \times 10^{5}+2.21 \times 4.2 \times 10^{3} \times \theta=5.9 \times 4.2 \times 10^{3} \times(40-\theta)$
সমাধান করে, θ = 8.5°C
১০. পানি সাপেক্ষে কাঁচের প্রতিসারঙ্ক 9/8. বায়ু সাপেক্ষে কাঁচের প্রতিসরাঙ্ক 3/2, বায়ু সাপেক্ষে পানির প্রতিসারঙ্ক কত?
ক. 2/3
খ. 4/5
গ. 4/3
ঘ. 3/4
উত্তর : গ. 4/3
সামাধান :
$w \mu_{g}=a \mu_{g} / a \mu_{W}, \therefore a \mu_{W}=a \mu_{g} / w \mu_{g}=\frac{\frac{3}{2}}{\frac{9}{8}}=\frac{3 x 8}{2 x 9}=\frac{4}{3}$
১১. সরল ছন্দিত গতিতে চলমান একটি বস্তুর মোট শক্তি E, কম্পাঙ্ক অপরিবর্তিত রেখে বিস্তার দ্বিগুণ করলে সরল ছন্দিত গতিতে চলমান বস্তুটির মোট গতিশক্তি কত হবে?
ক. E
খ. 2E
গ. E/2
ঘ. 4E
উত্তর : ঘ. 4E
সামাধান :
গতি শক্তি, k = ½ K (A2 – x2), অর্থাৎ গতিশক্তি বিস্তারের বর্গের সমানুপাতিক
∴ A দ্বিগুণ করা হলে মোট গতিশক্তি (22)xE= 4E
১২. হাইড্রোজেন পরমাণুর শক্তি স্তরের প্রকাশ $\mathrm{E}=-\frac{13.5}{n^{2}} \mathrm{eV},(\mathrm{n}=1.2, \ldots)$. ভূমি অবস্থা থেকে পরবর্তী উচ্চতর শক্তিস্তরে যেতে একটি হাইড্রোজেন পরমাণু কি পরিমাণ শক্তি শোষণ করে?
ক. 3.4 eV
খ. 4.5 eV
গ. 10.2 eV
ঘ. 13.6 eV
উত্তর : ক. 3.4 eV
সামাধান :
n = 2 হলে $\mathrm{E}=\frac{13.5}{2^{2}} \mathrm{eV}=3 \cdot 4 \mathrm{eV}$
১৩. একটি কণার ভরবেগ P, কণাটির গতিশক্তি দ্বিগুণ করা হলে এর নতুন ভরবেগ কত হবে?
ক.  2P
2P
খ. 2P
গ. 4P
ঘ. 8P
উত্তর : ক.  2P
2P
সামাধান :
$\mathrm{E}=\frac{1}{2} \mathrm{x} \frac{p^{2}}{m}, \mathrm{E} \propto \mathrm{P}^{2} \therefore 2 \mathrm{E}$ এর জন্য নতুন ভরবেগ (√2P)
১৪. 100 W ক্ষমতা সম্পন্ন একটি হিটারে 2 kg ভরের একটি কপারের খণ্ডকে 40 s তাপ দেয়া হলে খণ্ডটির তাপমাত্রা কত বৃদ্ধি হবে? কপারের আপেক্ষিক তাপ 400 J/(Kg K)
ক. 5 K
খ. 10 K
গ. 20 K
ঘ. 50 K
উত্তর : ক. 5 K
সামাধান :
$\mathrm{Q}=\mathrm{Pt}=100 \times 40=4000, \therefore \Delta \theta=\frac{4000}{2 \times 400}=5 \mathrm{~K}$
১৫. 300 Hz কম্পাঙ্কের এবং বিপরীত দিকে অগ্রগামী দুটি অভিন্ন তরঙ্গের উপরিপাতনের ফলে একটি স্থির তরঙ্গের সৃষ্টি হয়েছে। স্থির তরঙ্গের পর পর দুটি নিস্পন্দ বিন্দুর দূরত্ব 1.5 m. অগ্রগামী তরঙ্গ দুটির বেগ কত?
ক. 100 m/s
খ. 200 m/s
গ. 450 m/s
ঘ. 900 m/s
উত্তর : ঘ. 900 m/s
সামাধান :
১৬. একটি কৈশিক নলের ব্যাস 0.04x10-4m. এর এক প্রান্ত পানিতে ডুবালে পানি নলের ভিতর 0.082 m উপরে উঠে। পানির তল টান কত? দেওয়া আছে, স্পর্শ কোণ = 0°C এবং পানির ঘনত্ব = 1.0x103 Kg/m3
ক. 8.5 x 10-4 N/m
খ. 7.5 x 10-4 N/m
গ. 9.0 x 10-4 N/m
ঘ. 8.0 x 10-4 N/m
উত্তর : ঘ. 8.0 x 10-4 N/m
সামাধান :
$\mathrm{T}=\frac{\mathrm{hr} \rho \mathrm{g}}{2 \cos \theta}, \mathrm{T}=\frac{0.082 \times 0.02 \times 10^{-4} \times 10^{3} \times 9.8}{2}=8.0 \times 10^{-4}$
১৭. একটি ধারকের দুই পাতের মধ্যে বিভব পার্থক্য V এবং ধারকের সঞ্চিত শক্তি X, ধারকের বিভব পার্থক্য বৃদ্ধি করে 3V করা হলে সঞ্চিত শক্তি বৃদ্ধি পেয়ে কত হবে?
ক. 3 X
খ. 6 X
গ. 9 X
ঘ. 27 X
উত্তর : গ. 9 X
সামাধান :
$\mathrm{E}=\frac{1}{2} \mathrm{CV}^{2}, 3 \mathrm{~V}$ করা হলে সঞ্চিত শক্তি বৃদ্ধি পেয়ে হবে $9X$
১৮. একটি ${ }^{238}{ }_{93} \mathrm{~U}$ নিউক্লিয়াস দুই ধাপে ক্ষয় হয়ে ${ }^{234}{ }_{91} \mathrm{~Pa}$ নিউক্লিয়াস সৃষ্টি করে। এই দুই ধাপে কী কী ধরনের রশ্মি নির্গত হয়?
ক. α and ß
খ. α and γ
গ. ß and ß
ঘ. ß and γ
উত্তর :
১৯. একটি কমন এমিটার ট্রানজিস্টারের ß = 100 এবং IB = 50 µA হলে α কত?
ক. 1.01
খ. 0.99
গ. 1.00
ঘ. 1.10
উত্তর : খ. 0.99
সামাধান :
$\beta=\frac{\Delta \mathrm{I}_{\mathrm{C}}}{\Delta \mathrm{I}_{\mathrm{B}}} \therefore \mathrm{I}_{\mathrm{C}}=100 \times 50 \times 10^{-6}=0.005, \therefore \mathrm{I}_{\mathrm{E}}=0.00005+0.005=0.00505$,
$\therefore \alpha=\frac{0.005}{0.00505}=0.99$
২০. একটি গাড়ি সোজা উত্তর দিকে 90 m পথ 15 s সময়ে অতিক্রম করে। পরবর্তীতে গাড়িটি দ্রুত ঘুরে দক্ষিণ দিকে 40 m দূরত্ব 5 s সময়ে অতিক্রম করে। এই 20 s সময়কালে গাড়িটির গড় বেগের মান কত?
ক. 2.5 m/s
খ. 5.0 m/s
গ. 6.5 m/s
ঘ. 7.0 m/s
উত্তর : গ. 6.5 m/s
সামাধান :
130/20 = 6.5
২১. একটি তারের উপর টান F হলে দৈর্ঘ্যবৃদ্ভি হয় x, তারটি যদি হুকের সূত্র মেনে চলে এবং তারের উপাদানের ইয়ং গুণাঙ্ক Y হয় তবে তারে সঞ্চিত বিভব শক্তি কত?
A. $\frac{1}{2} \mathrm{Yx}$
B. $\mathrm{Yx}$
C. $\frac{1}{2} \mathrm{Fx}$
D. $\mathrm{Fx}$
উত্তর : C. $\frac{1}{2} \mathrm{Fx}$
সামাধান :
$w=\frac{1}{2} \times \frac{Y A l^{2}}{L}$ , এখানে, $\mathrm{Y}=\frac{F L}{A x}$  বা
বা  $\frac{A}{\mathrm{~L}}=\frac{F}{Y x}, \mathrm{~W}=\frac{1}{2} \mathrm{x} \frac{Y F x^{2}}{Y x}=\frac{1}{2} \mathrm{Fx}$
$\frac{A}{\mathrm{~L}}=\frac{F}{Y x}, \mathrm{~W}=\frac{1}{2} \mathrm{x} \frac{Y F x^{2}}{Y x}=\frac{1}{2} \mathrm{Fx}$
২২. তোমার একটি 15Ω রোধ প্রয়োজন কিন্তু তোমার কাছে কয়েকটি 10Ω রোধ আছে। কীভাবে তুমি 10Ω রোধ ব্যবহার করে 15Ω রোধটি তৈরি করবে?
ক. তিনটি সমান্তরাল সংযোগে
খ. তিনটি শ্রেণীবদ্ধ সংযোগে
গ. দুটি শ্রেণীবদ্ধ সংযোগে
ঘ. দুটি সমান্তরাল সংযোগে এবং একটি শ্রেণিবদ্ধ সংযোগে
উত্তর : ঘ. দুটি সমান্তরাল সংযোগে এবং একটি শ্রেণিবদ্ধ সংযোগে
সামাধান :
$10+\frac{1}{10^{-1}+10^{-1}}=15$
২৩. বলবিদ্যার বিভিন্ন মৌলিক ভৌত রাশি সমূহ হল?
ক. ভর, বল এবং সময়
খ. ভর, দৈর্ঘ্য এবং সময়
গ. বল, শক্তি এবং সময়
ঘ. বল, ভর এবং সময়
উত্তর : খ. ভর, দৈর্ঘ্য এবং সময়
২৪. একই দৈর্ঘ্য এবং একই পদার্থ দিয়ে তৈরি দুটি তার P এবং Q কে একটি ব্যাটারির সাথে সমান্তরালে সংযুক্ত করা হয়েছে। P তারের ব্যাস 2mm এবং Q তারের ব্যাস 1mm. P এবং Q এর তড়িৎ প্রবাহের অনুপাত কত?
ক. 1/4
খ. 1/2
গ. 2/1
ঘ. 4/1
উত্তর : ঘ. 4/1
সামাধান :
$\frac{l_{1}}{l_{2}}=\frac{R_{2}}{R_{1}}=\frac{A_{1}}{A_{2}}=\left(\frac{r_{1}}{r_{2}}\right)^{2}=\left(\frac{d_{1}}{d_{2}}\right)^{2}=\frac{4}{1}$
২৫. 5 kg ভরের একটি রাইফেল থেকে 20 g ভরের একটি বুলেট 1000 m/s গতিতে ছুটে যায়। পিছন দিকে রাইফেলের ধাক্কার বেগ কত?
ক. 4 m/s
খ. 4000 m/s
গ. 400 m/s
ঘ. 40 m/s
উত্তর : ক. 4 m/s
সামাধান :
$\mathrm{V}=\frac{0.02 \times 1000}{5}=4$
২৬. একটি পাথরকে স্থির অবস্থায় একটি উঁচু দালান থেকে ছেড়ে দেওয়া হল। ভূমিতে পৌছাতে পাথরটির 4 s এর বেশি সময় লাগে। বাতাসের ঘর্ষণ ক্ষুদ্র হলে পাথরটির প্রথম 4 s সময়ে পতনের দূরত্ব এবং প্রথম 2 s সময়ে পতনের দূরত্বের অনুপাত কত?
ক. 1/4
খ. 4/1
গ. 1/2
ঘ. 2/1
উত্তর : খ. 4/1
সামাধান :
$\mathrm{h}=\frac{1}{2} \mathrm{gt}^{2}, \therefore \frac{h_{1}}{h_{2}}=\left(\frac{t_{1}}{t_{2}}\right)^{2}=\frac{4}{1}$
২৭. চিত্রে একটি বর্তনীতে সমান্তরাল সন্নিবেশে সংযুক্ত তিনটি রোধ দেখানো হয়েছে। ব্যাটারির তড়িৎ-চালক শক্তি 12 V এবং অভ্যন্তরীণ রোধ নগন্য। অ্যামিটারের পাঠ 3.2 A হলে, X এর রোধ কত?
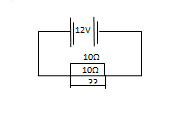
ক. 2.1 Ω
খ. 4.6 Ω
গ. 6.0 Ω
ঘ. 15 Ω
উত্তর : ঘ. 15 Ω
সামাধান :
$\mathrm{R}=\frac{12}{3.2}=3.75$ , আবার $\frac{1}{10^{-1}+10^{-1}+15^{-1}}=3.75$
২৮. একটি বস্তুকে অনুভূমির সাথে 30° কোণে নিক্ষেপ করা হল। পরবর্তীতে একই বস্তুকে একই আদি দ্রুতিতে অনুভূমির সাথে 40° কোণে নিক্ষেপ করা হল। নিম্নের কোনটি সত্য নয়
ক. অনুভূমিক পাল্লা বৃদ্ভি পেল
খ. বেগের অনুভূমিক উপাংশ বৃদ্ধি পেল
গ. সর্বোচ্চ উচ্চতা বৃদ্ধি পেল
ঘ. বস্তুটির উড্ডয়নকাল বৃদ্ধি পেল
উত্তর : খ. বেগের অনুভূমিক উপাংশ বৃদ্ধি পেল
সামাধান :
বেগের অনুভূমিক উপাংশ, $\mathrm{V}_{0} \cos \theta_{0}$ , এবং $\cos 30^{\circ}>\cos 40^{\circ}$
২৯. একটি আদর্শ ট্রান্সফর্মারের গৌণ ও মূখ্য কুণ্ডলীর পাক সংখ্যার অনুপাত 6:1. যদি মুখ্য কুণ্ডলীতে প্রতি সেকেন্ডে ব্যয়িত শক্তি 6 J হয়, তবে গৌণ কুণ্ডলীতে বৈদ্যুতিক ক্ষমতা কত?
ক. 6 J
খ. 36 Js-1
গ. 6 W
ঘ. 36 W
উত্তর : গ. 6 W
সামাধান :
মুখ্য ও গৌণ কুণ্ডলীতে বৈদ্যুতিক ক্ষমতা সমান।
৩০. m ভরের একটি বস্তু r ব্যাসার্ধের বৃত্তাকার পথে সমদ্রুতিতে চলছে। বৃতাকার গতির পর্যায়কাল T, বস্তুটির উপর কেন্দ্রমুখী বলের মান কত?
ক. 4π2mr/T2
খ. 4π2mr/T
গ. 4πmr2/T2
ঘ. πmr2
উত্তর : ক. 4π2mr/T2
সামাধান :
$\mathrm{F}=\mathrm{m} \alpha, \alpha=\omega^{2} \mathrm{r}=\left(\frac{2 \pi}{\tau}\right)^{2} \times r \therefore F=\frac{4 \pi^{2} m r}{\tau^{2}}$
গণিত
1. y = mx, y = m1x এবং y = b সরলরেখাত্রয় দ্বারা গঠিত ত্রিভুজের বর্গএককে ক্ষেত্রফল হবে
(A) $\frac{\mathrm{b}^{2}\left(\mathrm{~m}_{1}-\mathrm{m}\right)}{2 \mathrm{~mm}_{1}}$
(B) $\frac{\mathrm{b}^{2}\left(\mathrm{~m}-\mathrm{m}_{1}\right)}{2 \mathrm{~mm}_{1}}$
(C) $\frac{\mathrm{b}^{2}\left|\mathrm{~m}-\mathrm{m}_{1}\right|}{\mathrm{mm}_{1}}$
(D) $\frac{\mathrm{b}^{2}\left|\mathrm{~m}-\mathrm{m}_{1}\right|}{2 \mathrm{~mm}_{1}}$
Answer: (D) $\frac{\mathrm{b}^{2}\left|\mathrm{~m}-\mathrm{m}_{1}\right|}{2 \mathrm{~mm}_{1}}$
সামাধান :
$\mathrm{O} \equiv(\mathrm{o}, \mathrm{o})$
$\mathrm{A} \equiv\left(\frac{\mathrm{b}}{\mathrm{m}}, \mathrm{b}\right)$
$\mathrm{B} \equiv\left(\frac{\mathrm{b}}{\mathrm{m}_{1}}, \mathrm{~b}\right)$
$\Delta \mathrm{OAB}=\frac{1}{2}\left|\begin{array}{ccc}0 & 0 & 1 \\ \frac{\mathrm{b}}{\mathrm{m}} & \mathrm{b} & 1 \\ \frac{\mathrm{b}}{\mathrm{m}_{1}} & \mathrm{~b} & 1\end{array}\right|=\frac{1}{2}\left(\frac{\mathrm{b}^{2}}{\mathrm{~m}}-\frac{\mathrm{b}^{2}}{\mathrm{~m}_{1}}\right)=\frac{\mathrm{b}^{2}\left|\mathrm{~m}-\mathrm{m}_{1}\right|}{2 \mathrm{~mm}_{1}}$
Answer: (D) $\frac{\mathrm{b}^{2}\left|\mathrm{~m}-\mathrm{m}_{1}\right|}{2 \mathrm{~mm}_{1}}$
2. 3x2 + 5y2 = 15 উপবৃত্তের উৎকেন্দ্রিকতা হবে
(A) $\sqrt{3 / 5}$
(B) $\sqrt{5 / 3}$
(C) $\sqrt{2 / 5}$
(D) $\sqrt{5 / 2}$
Answer: (C) $\sqrt{2 / 5}$
সামাধান :
$3 x^{2}+5 y^{2}=15$
$\Rightarrow \frac{3 x^{2}}{15}+\frac{5 y^{2}}{15}=0$
$\Rightarrow \frac{x^{2}}{5}+\frac{y^{2}}{3}=0$
$\therefore a^{2}=5, b^{2}=3$
$\because a>b$
$\mathrm{e}^{2}=\frac{\mathrm{a}^{2}-\mathrm{b}^{2}}{\mathrm{a}^{2}}=\frac{5-3}{5}=\frac{2}{5}$
$\therefore e=\sqrt{\frac{2}{5}}$
Answer: (C) $\sqrt{2 / 5}$
3. $\left(2 x^{2}-\frac{1}{2 x^{3}}\right)^{10}$ এর বিস্তৃতিতে x-বর্জিত পদটি কততম এবং এর মান কত?
(A) পঞ্চম এবং 840
(B) চতুর্থ এবং 1920
(C) ষষ্ট এবং 252
(D) সপ্তম এবং 30
Answer: (A) পঞ্চম এবং 840
সামাধান :
(r + 1) তম পদ হবে
${ }^{10} \mathrm{C}_{\mathrm{r}}\left(2 \mathrm{x}^{2}\right)^{10-\mathrm{r}}\left(-\frac{1}{2 \mathrm{x}^{3}}\right)^{\mathrm{r}}$
$=10 \mathrm{C}_{\mathrm{r}} \cdot 2^{10-\mathrm{r}} \cdot \mathrm{x}^{20-2 \mathrm{r}} \cdot(-1)^{\mathrm{r}} \cdot 2^{-\mathrm{r}} \cdot \mathrm{x}^{-3 \mathrm{r}}$
$=(-1)^{\mathrm{r}} \cdot{ }^{10} \mathrm{C}_{\mathrm{r}} \cdot 2^{10-2 \mathrm{r}} \cdot \mathrm{x}^{20-5 \mathrm{r}}$
যদি পদটি x বর্জিত হয় তবে
$20-5 r=0 \Rightarrow 5 r=20 \Rightarrow r=4$
∴ (r + 1) = 5-তম পদ x বর্জিত এবং এর মান হবে
$(-1)^{4} \cdot{ }^{10} \mathrm{C}_{4} \cdot 2^{2}=840$
Answer: (A) পঞ্চম এবং 840
4. একটি বস্তুর খাড়া উপরের দিকে প্রক্ষেপন করলে নির্দিষ্ট বিন্দু P-তে পৌছাতে t1 সময় লাগে। যদি আরও t2 সময় পর বস্তুটি ভূমিতে পতিত হয় তবে কণাটির সর্বোচ্চ উচ্চতা হবে
(A) $\frac{1}{2} \mathrm{~g}\left(\mathrm{t}_{1}+\mathrm{t}_{2}\right)^{2}$
(B) $\frac{1}{8} \mathrm{~g}\left(\mathrm{t}_{1}+\mathrm{t}_{2}\right)^{2}$
(C) $\frac{1}{2} \mathrm{~g}\left(\mathrm{t}_{1}{ }^{2}+\mathrm{t}_{2}{ }^{2}\right)$
(D) $\frac{1}{8} \mathrm{~g}\left(\mathrm{t}_{1}{ }^{2}+\mathrm{t}_{2}{ }^{2}\right)$
Answer: (B) $\frac{1}{8} \mathrm{~g}\left(\mathrm{t}_{1}+\mathrm{t}_{2}\right)^{2}$
সামাধান :
মোট বিচরণকাল = T = t1 + t2
আবার,
$\mathrm{T}=\frac{2 \mathrm{u}}{\mathrm{g}}$
$\Rightarrow \mathrm{u}=\frac{1}{2} \mathrm{~g} \mathrm{~T}=\frac{1}{2} \mathrm{~g}\left(\mathrm{t}_{1}+\mathrm{t}_{2}\right)$
$\Rightarrow \mathrm{u}^{2}=\frac{1}{4} \mathrm{~g}^{2}\left(\mathrm{t}_{1}+\mathrm{t}_{2}\right)^{2}$
∴ সর্বোচ্চ উচ্চতা হবে
$\frac{u^{2}}{2 g}=\frac{1}{8} g\left(t_{1}+t_{2}\right)^{2}$
Answer: $(\mathrm{B}) \frac{1}{8} \mathrm{~g}\left(\mathrm{t}_{1}+\mathrm{t}_{2}\right)^{2}$
5. $\tan \left(\tan ^{-1}\left(\frac{1}{3}\right)+\tan ^{-1}\left(\frac{1}{2}\right)\right)$ এর মান হবে
(A) $\frac{5}{6}$
(B) $1$
(C) $\frac{\pi}{4}$
(D) $-\frac{5}{6}$
Answer: (B) $1$
সামাধান :
সারাসরি Calculator ব্যবহার করে:
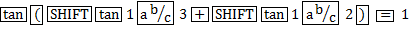
6. $\left|\begin{array}{lll}\mathrm{a} & 1 & \mathrm{~b}+\mathrm{c} \\ \mathrm{b} & 1 & \mathrm{c}+\mathrm{a} \\ \mathrm{c} & 1 & \mathrm{a}+\mathrm{b}\end{array}\right|$ এর মান হবে
(A) 0
(B) $a b c(a+b)(b+c)(c+a)$
(C) abc
(D) $(\mathrm{a}+\mathrm{b})(\mathrm{b}+\mathrm{c})(\mathrm{c}+\mathrm{a})$
Answer: (A) o
সামাধান :
$\left|\begin{array}{lll}\mathrm{a} & 1 & \mathrm{~b}+\mathrm{c} \\ \mathrm{b} & 1 & \mathrm{c}+\mathrm{a} \\ \mathrm{c} & 1 & \mathrm{a}+\mathrm{b}\end{array}\right|$
$=\left|\begin{array}{lll}a+b+c & 1 & b+c \\ a+b+c & 1 & c+a \\ a+b+c & 1 & a+b\end{array}\right|$
$=a+b+c\left|\begin{array}{lll}1 & 1 & b+c \\ 1 & 1 & c+a \\ 1 & 1 & a+b\end{array}\right| \quad\left[c_{1}^{\prime}=c_{1}+c_{3}\right]$
$=0$
Answer: (A) $0$
7. 3P এবং 2P বলদ্বয়ের লব্ধি R। প্রথম বল দ্বিগুণ করলে লব্ধির পরিমাণও দ্বিগুণ হয়। বলদ্বয়ের অন্তর্গত কোণ হবে
(A) 110°
(B) 120°
(C) 150°
(D) 135°
Answer: (B) 120°
সামাধান :
মনে করি, 3P এবং 2P মানের বলদ্বয়ের অন্তর্গত কোণ α।
$\therefore \mathrm{R}^{2}=9 \mathrm{P}^{2}+4 \mathrm{P}^{2}+12 \mathrm{P}^{2} \cos \alpha=13 \mathrm{P}^{2}+12 \mathrm{P}^{2} \cos \alpha$
প্রথম বলের মান দ্বিগুণ করলে
$4 \mathrm{R}^{2}=(6 \mathrm{P})^{2}+4 \mathrm{P}^{2}+2.2 \mathrm{P} .6 \mathrm{P} \cos \alpha=36 \mathrm{P}^{2}+4 \mathrm{P}^{2}+24 \mathrm{P}^{2} \cos \alpha=40 \mathrm{P}^{2}+24 \mathrm{P}^{2} \cos \alpha$
$\therefore \frac{4 \mathrm{R}^{2}}{\mathrm{R}^{2}}=\frac{\mathrm{P}^{2}(40+24 \cos \alpha)}{\mathrm{P}^{2}(13+12 \cos \alpha)}$
$\Rightarrow 52+48 \cos \alpha=40+24 \cos \alpha$
$\Rightarrow 24 \cos \alpha=-12$
$\Rightarrow \cos \alpha=-1 / 2$
$\therefore \alpha=120^{\circ}$
Answer: (B) $120^{\circ}$
8. একটি ইলেকট্রিক ফিল্ডে ইলেকট্রনের ত্বরণ এবং শক্তি সমানুপাতিক। $10^{-20} \mathrm{~N}$ শক্তির জন্য ত্বরণ $10^{10} \frac{\mathrm{m}}{\mathrm{s}^{2}}$ হলে, $10^{-25} \mathrm{~N}$ শক্তির জন্য ত্বরণ হবে
(A) $10^{5} \mathrm{~m} / \mathrm{s}^{2}$
(B) $10^{15} \mathrm{~m} / \mathrm{s}^{2}$
(C) $10^{-5-} \mathrm{m} / \mathrm{s}^{2}$
(D) $10^{-15} \mathrm{~m} / \mathrm{s}^{2}$
Answer: (A) $10^{5} \mathrm{~m} / \mathrm{s}^{2}$
সামাধান :
দেওয়া আছে, ত্বরণ ∝ শক্তি
$10^{10} \mathrm{~m} / \mathrm{s}^{2} \propto 10^{-20} \mathrm{~N}$
আবার,
$x \propto 10^{-25}$
$\therefore \frac{x}{10^{10}}=\frac{10^{-25}}{10^{-20}}$
$\Rightarrow \mathrm{x}=10^{-25} \cdot 10^{10} \cdot 10^{20}=10^{5}$
Answer: (A) $10^{5} \mathrm{~m} / \mathrm{s}^{2}$
9. দশমিক সংখ্যা $2013$ এর দ্বিমিকে প্রকাশ হবে
(A) 11111011101
(B) 10111011111
(C) 10101110111
(D) 10101110101
Answer: (A) 11111011101
সামাধান :
$2 \mid 2012$
$2 \mid 1006-1$
$2 \mid 503-0$
$2 \mid 251-1$
$2 \mid 125-1$
$2 \mid 62-1$
$2 \mid 31-0$
$2 \mid 15-1$
$2 \mid 7-1$
$2 \mid 3-1$
$2 \mid 1-1$
$0-1$
$\therefore(2013)_{10}=(11111011101)_{2}$
Answer: (A) 11111011101
10. x = y2 এবং y = x ‒ 2 দ্বারা আবদ্ধ ক্ষেত্রের ক্ষেত্রফল হবে
(A) $1 \frac{1}{3}$
(B) $1 \frac{1}{3}$
(C) $4 \frac{1}{2}$
(D) $4 \frac{3}{4}$
Answer: (C) $4 \frac{1}{2}$
সামাধান :
$\mathrm{x}=\mathrm{y}^{2}$
$\mathrm{y}=\mathrm{x}-2 \Rightarrow \mathrm{x}=\mathrm{y}+2$
$\therefore \mathrm{y}^{2}=\mathrm{y}+2$
$\Rightarrow \mathrm{y}^{2}-\mathrm{y}-2=0$
$\Rightarrow \mathrm{y}^{2}-2 \mathrm{y}+\mathrm{y}-2=0$
$\Rightarrow \mathrm{y}(\mathrm{y}-2)+1(\mathrm{y}-2)=0$
$\Rightarrow(\mathrm{y}-2)(\mathrm{y}+1)=0$
$\Rightarrow \mathrm{y}=-1,2$
$\int_{-1}^{2}\left(\mathrm{y}+2-\mathrm{y}^{2}\right) \mathrm{dy}$
$=\int_{-1}^{2} \mathrm{y} \mathrm{dy}+2 \int_{-1}^{2} \mathrm{dy}-\int_{-1}^{2} \mathrm{y}^{2} \mathrm{dy}$
$=\left[\frac{1}{2} y^{2}\right]_{-1}^{2}+[2 y]_{-1}^{2}-\left[\frac{1}{3} y^{3}\right]_{-1}^{2}$
$=\frac{1}{2}(4-1)+2(2+1)-\frac{1}{3}(8+1)$
$=4 \frac{1}{2}$
Answer: (C) $4 \frac{1}{2}$
11. যদি $y=\sqrt{\cos 2 x}$ হয়, তবে $\frac{d y}{d x}=$
(A) $-\frac{\sin 2 x}{\sqrt{\cos 2 x}}$
(B) $-\frac{\cos 2 x}{\sqrt{\sin 2 x}}$
(C) $-\frac{2 \sin 2 x}{\sqrt{\tan x}}$
(D) $\frac{\tan 2 \mathrm{x}}{\sqrt{\sin 2 \mathrm{x}}}$
Answer: (A) $-\frac{\sin 2 x}{\sqrt{\cos 2 x}}$
সামাধান :
$\mathrm{y}=\sqrt{\cos 2 \mathrm{x}}$ $\frac{d y}{d x}=\frac{1}{2 \sqrt{\cos 2 \mathrm{x}}} \frac{d}{d x} \cos 2 \mathrm{x}=\frac{1}{2 \sqrt{\cos 2 \mathrm{x}}}(-\sin 2 \mathrm{x}) \frac{d}{d x} 2 \mathrm{x}=-\frac{\sin 2 \mathrm{x}}{\sqrt{\cos 2 \mathrm{x}}}$ Answer: (A) $-\frac{\sin 2 \mathrm{x}}{\sqrt{\cos 2 \mathrm{x}}}$
12. একজন কৃষক একটি আয়তাকার বাগানের তিন দিক বেড়া দিয়ে এবং চতুর্দিকে একটি দেওয়াল দিয়ে ঘেরাও দিল। যদি তাঁর কাছে $100 m$ বেড়া থাকে তবে ঘেরাও দেওয়া স্থানের সর্বোচ্চ আয়তন হবে
(A) 2500 m2
(B) 1250 m2
(C) 750 m2
(D) 2000 m2
Answer: (B) 1250 m2
13. sin (ax + b) এর n-তম অন্তরক হবে
(A) $a^{n} \sin \left(\frac{\pi}{2} n+a x+b\right)$
(B) $a^{n} \cos \left(\frac{\pi}{2} n+a x+b\right)$
(C) $(-1)^{\mathrm{n}} a^{\mathrm{n}} \sin (a x+b)$
(D) $(-1)^{\mathrm{n}} \mathrm{a}^{\mathrm{n}} \cos (\mathrm{ax}+\mathrm{b})$
Answer: (A) $a^{n} \sin \left(\frac{\pi}{2} n+a x+b\right)$
সামাধান :
$y=\sin (a x+b)$
$y_{1}=a \cos (a x+b)=a \sin \left(\frac{\pi}{2}+a x+b\right)$
$y_{2}=a^{2} \cos \left(\frac{\pi}{2}+a x+b\right)=a^{2} \sin \left(2 \cdot \frac{\pi}{2}+a x+b\right)$
$y_{3}=a^{3} \cos \left(2 \cdot \frac{\pi}{2}+a x+b\right)=a^{3} \sin \left(3 \cdot \frac{\pi}{2}+a x+b\right)$
-------------------------------------------------
$\therefore \mathrm{y}_{\mathrm{n}}=\mathrm{a}^{\mathrm{n}} \sin \left(\frac{\pi}{2} \mathrm{n}+\mathrm{ax}+\mathrm{b}\right)$
Answer: $(A) a^{n} \sin \left(\frac{\pi}{2} n+a x+b\right)$
14. ‘a’ এর কোন মানের জন্য $2 \hat{\imath}+\hat{\jmath}-\hat{k}, 3 \hat{\imath}-2 \hat{\jmath}+4 \hat{k}$ এবং $\hat{\imath}-3 \hat{\jmath}+a \hat{k}$ ভেক্টরত্রয় সমতলীয়?
(A) 5
(B) 4
(C) 3
(D) 2
Answer: (A) 5
সামাধান :
$\left|\begin{array}{ccc}2 & 1 & -1 \\ 3 & -2 & 4 \\ 1 & -3 & a\end{array}\right|=0$
$\Rightarrow\left|\begin{array}{ccc}0 & 0 & -1 \\ 11 & 2 & 4 \\ 2 a+1 & a-3 & a\end{array}\right|=0$
$\Rightarrow-(11 a-33-4 a-2)=0$
$\Rightarrow 7 a-35=0$
$\therefore a=5$
Answer: (A) 5
15. $8+4 \sqrt{5} i$ এর বর্গমূল হবে
$(\mathrm{A}) \pm(3-2 \mathrm{i})$
(B) $\pm \sqrt{10}+\sqrt{2} \mathrm{i}$
(C) $\pm \sqrt{10}-\sqrt{2} \mathrm{i}$
(D) $\pm(3+2 i)$
Answer: (B) $\pm \sqrt{10}+\sqrt{2} \mathrm{i}$
সামাধান :
$a=8$
$b=4 \sqrt{5}$
$(8+4 \sqrt{5} i)^{\frac{1}{2}}$
$=\pm\left[\left\{\frac{1}{2}\left(\sqrt{a^{2}+b^{2}}+a\right)\right\}^{\frac{1}{2}}+i\left\{\frac{1}{2}\left(\sqrt{a^{2}+b^{2}}-a\right)\right\}^{\frac{1}{2}}\right]$
$=\pm\left\{\frac{1}{2}(8+\sqrt{64+80})\right\}^{\frac{1}{2}}+i\left\{\frac{1}{2}(-8+\sqrt{64+80})\right\}^{\frac{1}{2}}$
$=\pm\left\{\frac{1}{2}(8+12)\right\}^{\frac{1}{2}}+\mathrm{i}\left\{\frac{1}{2}(-8+12)\right\}^{\frac{1}{2}}$
$=\pm \sqrt{10}+\sqrt{2} \mathrm{i}$
Answer: (B) $\pm \sqrt{10}+\sqrt{2} \mathrm{i}$
16. যদি $x^{2}+3 x y+5 y^{2}=1$ হয়, তাহলে $\frac{d y}{d x}$ সমান হবে
(A) $-\frac{2 x+3 y}{3 x+10 y}$
(B) $\frac{2 x+3 y}{3 x+10 y}$
(C) $\frac{2 x-3 y}{3 x+10 y}$
(D) $\frac{2 x+3 y}{3 x-10 y}$
Answer: (A) $-\frac{2 x+3 y}{3 x+10 y}$
সামাধান :
$\mathrm{x}^{2}+3 \mathrm{xy}+5 \mathrm{y}^{2}=1$
$\Rightarrow 2 \mathrm{x}+3 \mathrm{y}+3 \mathrm{x} \frac{\mathrm{dy}}{\mathrm{dx}}+10 \mathrm{y} \frac{\mathrm{dy}}{\mathrm{dx}}=0$
$\Rightarrow \frac{d y}{d x}(3 x+10 y)=-(2 x+3 y)$
$\Rightarrow \frac{\mathrm{dy}}{\mathrm{dx}}=-\frac{2 \mathrm{x}+3 \mathrm{y}}{3 \mathrm{x}+10 \mathrm{y}}$
Answer: $(\mathrm{A})-\frac{2 \mathrm{x}+3 \mathrm{y}}{3 \mathrm{x}+10 \mathrm{y}}$
17. $\frac{1}{2}+\frac{1}{3^{2}}+\frac{1}{2^{8}}+\frac{1}{3^{4}}+\frac{1}{2^{5}}+\frac{1}{3^{6}}+\cdots$ ধারার সমষ্টি হবে
(A) $\frac{24}{19}$
(B) $\frac{19}{24}$
(C) $\frac{5}{24}$
(D) $\frac{5}{19}$
Answer: (B) $\frac{19}{24}$
18. $x^{2}-5 x-3=0$ সমীকরণের মূলদ্বয় $α$, $β$ হলে $\frac{1}{\alpha}, \frac{1}{\beta}$ মূলবিশিষ্ট সমীকরণটি হবে?
(A) $3 x^{2}-5 x+1=0$
(B) $x^{2}+5 x+3=0$
(C) $5 x^{2}-3 x-1=0$
(D) $3 \mathrm{x}^{2}+5 \mathrm{x}-1=0$
Answer: (D) $3 x^{2}+5 x-1=0$
সামাধান :
$a x^{2}+b x+c=0$ সমীকরণের মূলদ্বয় $alpha$ ও $beta$ হলে $\frac{1}{\alpha}$ ও $\frac{1}{\beta}$ মূলবিশিষ্ট সমীকরণ হবে, $c x^{2}+b x+a=0$
Answer: (D) 3x2 + 5x ‒ 1 = 0
19. বাস্তব সংখ্যায় $\frac{1}{|2 x-3|}>5$ অসমতাটির সমাধান হলো
(A) $\left(\frac{7}{5}, \frac{8}{5}\right)$
(B) $\left[\frac{7}{5}, \frac{8}{5}\right]$
(C) $\left(\frac{7}{5}, \frac{3}{2}\right) \cup\left(\frac{3}{2}, \frac{8}{5}\right)$
(D) $\left[\frac{7}{5}, \frac{3}{2}\right] \cup\left[\frac{3}{2}, \frac{8}{5}\right]$
Answer: (C) $\left(\frac{7}{5}, \frac{3}{2}\right) \cup\left(\frac{3}{2}, \frac{8}{5}\right)$
সামাধান :
$|2 x-3|<\frac{1}{5}$
$\Rightarrow-\frac{1}{5}<2 x-3<\frac{1}{5}$
$\Rightarrow \frac{7}{5}<x<\frac{8}{5}$
আবার, $x=\frac{3}{2}$ হলে $\frac{1}{|2 x-3|}=\frac{1}{0}$ অসংজ্ঞায়িত।
Answer: (C) $\left(\frac{7}{5}, \frac{3}{2}\right) \cup\left(\frac{3}{2}, \frac{8}{5}\right)$
20. মান নির্ণয় কর: $\lim _{x \rightarrow 0} \frac{e^{x}-1}{x}$
(A) 1
(B) $-1$
(C) 2
(D) 3
Answer: (A) 1
সামাধান :
l’Hôpital’s rule ব্যবহার করে পাই,
$\lim _{x \rightarrow 0} \frac{e^{x}-1}{x}=\lim _{x \rightarrow 0} e^{x}=1$
Answer: (A) 1
21. $\int \sqrt{\frac{1+x}{1-x}} d x=f(x)+c$ হলে, $\mathrm{f}(\mathrm{x})$ এর মান
(A) $\sin ^{-1} x+\sqrt{1-x^{2}}$
(B) $\sin ^{-1} x-\sqrt{1-x^{2}}$
(C) $\cos ^{-1} \mathrm{x}-\sqrt{1-\mathrm{x}^{2}}$
(D) $\sin ^{-1} x-\sqrt{1+x^{2}}$
Answer: (B) $\sin ^{-1} \mathrm{x}-\sqrt{1-\mathrm{x}^{2}}$
সামাধান :
$\int \sqrt{\frac{1+x}{1-x}} d x$
$=\int \frac{1+x}{\sqrt{1-x^{2}}} d x$
$=\int \frac{d x}{\sqrt{1-x^{2}}}+=\int \frac{x d x}{\sqrt{1-x^{2}}}$
$=\sin ^{-1} x-\sqrt{1-x^{2}}$
Answer: (B) $\sin ^{-1} \mathrm{x}-\sqrt{1-\mathrm{x}^{2}}$
22. $x^{2}+4 x+2 y=0$ পরাবৃত্তের শীর্ষবিন্দু হবে
(A) $(2,-2)$
(B) $(-2,-2)$
(C) $(-2,2)$
(D) $(2,2)$
Answer: (C) $(-2,2)$
সামাধান :
$\mathrm{x}^{2}+4 \mathrm{x}+2 \mathrm{y}=0$
$\Rightarrow(\mathrm{x}+2)^{2}=-2(\mathrm{y}-2) \ldots \ldots \ldots(\mathrm{i})$
ধরি,
$\mathrm{x}+2=\mathrm{X}, \mathrm{y}-2=\mathrm{Y}$
$(\mathrm{i}) \Rightarrow \mathrm{X}^{2}=-2 \mathrm{Y}$
শীর্ষবিন্দুর স্থানাঙ্ক: $\mathrm{X}=0, \mathrm{Y}=\mathrm{O}$
$\therefore \mathrm{x}=-2, \mathrm{y}=2$
Answer: (C) $(-2,2)$
23. $f(x)=4-(x-3)^{2}$ ফাংশনের ডোমেইন এবং রেইঞ্জ যথাক্রমে
(A) $\mathbf{R}, \mathbf{R}$
(B) $\mathbf{R}, \mathrm{x} \leq 4$
(C) $x \geq 4, \mathbf{R}$
(D) $\mathbf{R}, x \geq 3$
Answer: (B) $\mathbf{R}, x \leq 4$
সামাধান :
$\mathrm{x}$ এর সব বাস্তব মানের জন্য $f(x)$ এর বাস্তব মান পাওয়া যায়।
∴ ফাংশনের ডোমেইন = R
ধরি,
$y=f(x)=4-(x-3)^{2}$
$\Rightarrow(x-3)^{2}=4-y$
$\Rightarrow(x-3)=\pm \sqrt{4-y}$
$\Rightarrow x=3 \pm \sqrt{4-y}$
$\mathrm{y} \geq 4$ হলে $\mathrm{x}$ এর জটিল মান পাওয়া যায় যা ডোমেইন এর সদস্য নয়।
∴ $\mathrm{x}$ এর সব বাস্তব মানের জন্য $y \leq 4$ হবে।
∴ ফাংশনের রেইঞ্জ = $\{x: x \in \mathbf{R}$ এবং $x \leq 4\}$
Answer: (B) $\mathbf{R}, x \leq 4$
24. $\mathrm{x}$-অক্ষকে $(4, 0)$ বিন্দুতে স্পর্শ করে এবং কেন্দ্র $5 x-7 y+1=0$ সরলরেখার উপর অবস্থিত এমন বৃত্তের সমীকরণ হবে
(A) $x^{2}+y^{2}-8 x-6 y+9=0$
(B) $x^{2}+y^{2}-8 x+6 y+16=0$
(C) $x^{2}+y^{2}-8 x+6 y+9=0$
(D) $x^{2}+y^{2}-8 x-6 y+16=0$
Answer: (B) $x^{2}+y^{2}-8 x+6 y+16=0$
সামাধান :
ধরি, বৃত্তের সমীকরণ, $x^{2}+y^{2}+2 g x+2 f y+c=0$
∵ বৃত্তটি $\mathrm{x}$ অক্ষকে $(4,0)$ বিন্দুতে স্পর্শ করে ∴ কেন্দ্রের ভুজ $=4=-g$ এবং $c=g^{2}=16$
∵ কেন্দ্র $5 x-7 y+1=0$ রেখার উপর অবস্থিত $\therefore 5(4)-7(-f)+1=0 \Rightarrow f=3$
∴ বৃত্তের সমীকরণ, $x^{2}+y^{2}+2 g x+2 f y+c=0=x^{2}+y^{2}-8 x+6 y+16=0$
Answer: (B) $x^{2}+y^{2}-8 x+6 y+16=0$
25. $A=\left[\begin{array}{cc}1 & \mathrm{i} \\ -\mathrm{i} & 1\end{array}\right], B=\left[\begin{array}{cc}\mathrm{i} & -1 \\ -1 & -\mathrm{i}\end{array}\right]$ এবং $\mathrm{i}=\sqrt{-1}$ হলে $\mathrm{AB}$ এর মান হবে
(A) $\left[\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right]$
(B) $\left[\begin{array}{ll}0 & 0 \\ 0 & 0\end{array}\right]$
(C) $\left[\begin{array}{ll}\mathrm{i} & 0 \\ 0 & \mathrm{i}\end{array}\right]$
(D) $\left[\begin{array}{ll}\mathrm{i} & 1 \\ 1 & \mathrm{i}\end{array}\right]$
Answer: (B) $\left[\begin{array}{ll}0 & 0 \\ 0 & 0\end{array}\right]$
সামাধান :
$\mathrm{AB}$
$=\left[\begin{array}{cc}1 & \mathrm{i} \\ -\mathrm{i} & 1\end{array}\right] \times\left[\begin{array}{cc}\mathrm{i} & -1 \\ -1 & -\mathrm{i}\end{array}\right]$
$=\left[\begin{array}{cc}\mathrm{i}-\mathrm{i} & -1-\mathrm{i}^{2} \\ -\mathrm{i}^{2}-1 & \mathrm{i}-\mathrm{i}\end{array}\right]$
$=\left[\begin{array}{ll}0 & 0 \\ 0 & 0\end{array}\right]$
Answer: (B) $\left[\begin{array}{ll}0 & 0 \\ 0 & 0\end{array}\right]$
26. স্বরবর্ণগুলোকে সব সময় একত্রে রেখে KACHUA শব্দটির বর্ণগুলোকে সাজানোর সংখ্যা হবে
(A) 24
(B) 72
(C) 144
(D) 8
Answer: (B) 72
সামাধান :
KACHUA শব্দটিতে মোট বর্ণ $6$টি যার $3$টি স্বরবর্ণ। স্বরবর্ণ 3টি কে একটি বর্ণ ধরলে মোট বর্ণ হয় $(6 ‒ 3 + 1) = 4$ টি যাদেরকে $4 !$ উপায়ে সাজানো যায়। আরার স্বরবর্ণ 3টি কে নিজেদের মধ্যে $\frac{3 !}{2 !}$ উপায়ে সাজানো যায়।
∴ মোট বিন্যাস সংখ্যা $=4 ! \times \frac{3 !}{2 !}=72$
Answer: (B) 72
27. একজন লোকের $3$ জোড়া কালো মোজা এবং $2$ জোড়া বাদামী মোজা আছে। একদিন অন্ধকারে তাড়াহুড়া করে লোকটি কাপড় পরল। সে প্রথমে একটি বাদামী মোজা পরার পর পরবর্তী মোজাও বাদামী হওয়ার সম্ভাবনা
(A) $\frac{1}{3}$
(B) $\frac{2}{15}$
(C) $\frac{1}{10}$
(D) $\frac{3}{10}$
Answer: (C) $\frac{2}{15}$
সামাধান :
বাদামী মোজার সংখ্যা = 2×2 = 4
কালো মোজার সংখ্যা = 2×3 = 6
প্রথমে বাদামী মোজা পরার সম্ভব্যতা $=\frac{4}{10}=\frac{2}{5}$
পরে বাদামী মোজা পরার সম্ভব্যতা $=\frac{3}{9}=\frac{1}{3}$
প্রথমে একটি বাদামী মোজা পরার পর পরবর্তী মোজাও বাদামী হওয়ার সম্ভাবনা $\frac{2}{5} \times \frac{1}{3}=\frac{2}{15}$
Answer: (C) $\frac{2}{15}$
28. $\mathrm{f}(\mathrm{x})=\frac{\mathrm{x}-3}{2 \mathrm{x}+1}$ এবং $\mathrm{x} \neq \frac{1}{2}$ হলে $\mathrm{f}^{-1}(-2)$ এর মান কত হবে
(A) $\frac{1}{2}$
(B) $\frac{1}{5}$
(C) 2
(D) 5
Answer: (B) $\frac{1}{5}$
সামাধান :
ধরি,
$\mathrm{y}=\mathrm{f}(\mathrm{x})=\frac{\mathrm{x}-3}{2 \mathrm{x}+1}$
$\Rightarrow 2 \mathrm{xy}+\mathrm{y}=\mathrm{x}-3$
$\Rightarrow 2 \mathrm{xy}-\mathrm{x}=-\mathrm{y}-3$
$\Rightarrow \mathrm{x}=\frac{\mathrm{y}+3}{1-2 \mathrm{y}}$
$\mathrm{f}^{-1}(\mathrm{x})=\frac{\mathrm{x}+3}{1-2 \mathrm{x}}$
$f^{-1}(-2)=\frac{-2+3}{1-2(-2)}=\frac{1}{5}$
Answer: (B) $\frac{1}{5}$
29. $\mathrm{u}$ বেগে অনুভুমিকের সাথে $alpha$ কোণে প্রক্ষিপ্ত বস্তুর সর্বোচ্চ উচ্চতা হবে
(A) $\frac{\mathrm{u}^{2} \sin 2 \alpha}{2 \mathrm{~g}}$
(B) $\frac{\mathrm{u}^{2} \sin ^{2} \alpha}{2 \mathrm{~g}}$
(C) $\frac{\mathrm{u}^{2} \sin 2 \alpha}{\mathrm{g}}$
(D) $\frac{\mathrm{u}^{2} \sin ^{2} \alpha}{\mathrm{g}}$
Answer: (B) $\frac{\mathrm{u}^{2} \sin ^{2} \alpha}{2 \mathrm{~g}}$
30. $\frac{(i+1)^{2}}{(i-1)^{4}}$ জটিল সংখ্যাটির আর্গুমেন্ট হবে
(A) π
(B) ‒ π
(C) $\frac{\pi}{2}$
(D) ‒ $\frac{\pi}{2}$
Answer: (D) ‒ $\frac{\pi}{2}$
সামাধান :
$\frac{(i+1)^{2}}{(i-1)^{4}}$
$=\frac{(i+1)^{2}}{(i-1)^{2}(i-1)^{2}}$
$=\frac{\mathrm{i}^{2}+2 \mathrm{i}+1}{\left(\mathrm{i}^{2}-2 \mathrm{i}+1\right)\left(\mathrm{i}^{2}-2 \mathrm{i}+1\right)}$
$=\frac{2 \mathrm{i}}{(-2 \mathrm{i})(-2 \mathrm{i})}$
$=\frac{2 \mathrm{i}}{4 \mathrm{i}^{2}}$
$=-\frac{1}{2} \mathrm{i}$
∴ জটিল সংখ্যাটির আর্গুমেন্ট $-\frac{\pi}{2}$
Answer: (D) ‒ $\frac{\pi}{2}$
রসায়ন
1. নিম্নের কোন কোয়ান্টাম সেটটি পরমানুর একটি ইলেকট্রনের জন্য সম্ভব নয় ?
(A) $\mathrm{n}=2, \mathrm{I}=1, \mathrm{~m}=\mathrm{o}, \mathrm{s}=+1 / 2$
(B) $\mathrm{n}=3, \mathrm{l}=1, \mathrm{~m}=2, \mathrm{~s}=-1 / 2$
(C) $\mathrm{n}=1, \mathrm{I}=0, \mathrm{~m}=0, \mathrm{~s}=-1 / 2$
(D) $n=2, \mathrm{I}=0, \mathrm{~m}=0, \mathrm{~s}=+1 / 2$
উত্তর : (B) $\mathrm{n}=3, \mathrm{l}=1, \mathrm{~m}=2, \mathrm{~s}=-1 / 2$
2. হাইড্রোজেনের পারমাণবিক বর্ণালীর কোন সিরিজটিতে দৃশ্যমান অঞ্চলের রশ্মি দেখা যায় ?
(A) Paschen
(B) Lyman
(C) Balmer
(D) Brackett
উত্তর : (C) Balmer
3. $10.0g$ অক্সিজেনে অণুর সংখ্যা কত ?
(A) $3.76 \times 10^{23}$
(B) $6.02 \times 10^{22}$
(C) $9.63 \times 10^{23}$
(D) $1.88 \times 10^{23}$
উত্তর : (D) $1.88 \times 10^{23}$
4. নিম্নের কোনটির ব্যাসার্ধ সবচেয়ে কম ?
(A) $_{9} \mathrm{~F}^{-}$
(B) ${ }_{10} \mathrm{Ne}$
(C) ${ }_{11} \mathrm{Na}^{+}$
(D) $12 \mathrm{Mg}^{2+}$
উত্তর : (A) $_{9} \mathrm{~F}^{-}$
5. নিম্নের কোন যৌগটি সবচেয়ে কম তাপমাত্রায় বিয়োজিত হবে ?
(A) $\mathrm{Na}_{2} \mathrm{CO}_{3}$
(B) $\mathrm{K}_{2} \mathrm{CO}_{3}$
(C) $\mathrm{MgCO}_{3}$
(D) $\mathrm{BaCO}_{3}$
উত্তর : (C) $\mathrm{MgCO}_{3}$
6.নিম্নের কোন যৌগটির আকৃতি ত্রিকোণাকার সমতলীয় ?
(A) $\mathrm{BCl}_{3}$
(B) $\mathrm{H}_{3} \mathrm{O}^{+}$
(C) $\mathrm{BrF}_{5}$
(D) $\mathrm{PH}_{3}$
উত্তর : (A) $\mathrm{BCl}_{3}$
7. $300 k$ তাপমাত্রায় বাতাসের $\mathrm{N}_{2}$ অণুর গতি কত ?
(A) $450 \mathrm{~m} / \mathrm{s}$
(B) $516 \mathrm{~m} / \mathrm{s}$
(C) $400 \mathrm{~m} / \mathrm{s}$
(D) $600 \mathrm{~m} / \mathrm{s}$
উত্তর : (B) $516 \mathrm{~m} / \mathrm{s}$
8. গ্রিগনারড বিকারক হলো –
(A) CH3ONa
(B) RBaCl
(C) RMgX
(D) RCaX
উত্তর : (C) RMgX
9. ইথানলের $170^{\circ} \mathrm{C}$ তাপমাত্রায় অতিরিক্ত গাঢ় সালফিউরিক এসিড দ্বারা বিক্রিয়া করালে কী উৎপন্ন হয় ?
(A) $\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{SO}_{4}$
(B) $\mathrm{C}_{2} \mathrm{H}_{4} \mathrm{SO}_{4}$
(C) $\mathrm{CH}_{2}=\mathrm{CH}_{2}$
(D) $\mathrm{CH}_{3} \mathrm{CHO}$
উত্তর : (C) $\mathrm{CH}_{2}=\mathrm{CH}_{2}$
10. $10.0$ মি.লি. $\mathrm{NaOH}$ দ্রবণকে $0.12 \mathrm{M}$ ঘনমাত্রায় $15.0$ মি.লি অক্সালিক এসিড দ্বারা টাইট্রেশন করলে প্রশমন বিন্দু পাওয়া যায় । $\mathrm{NaOH}$ এর ঘনমাত্রা কত ?
(A) $0.25 \mathrm{M}$
(B) $0.36 \mathrm{M}$
(C) $0.32 \mathrm{M}$
(D) $0.40 \mathrm{M}$
উত্তর : (B) $0.36 \mathrm{M}$
11.ম্যানেসিয়াম ফসফেটের সংকেত হলো -
(A) $\mathrm{Mg}_{2}\left(\mathrm{PO}_{4}\right)_{2}$
(B) $\mathrm{MgPO}_{4}$
(C) $\mathrm{Mg}_{2}\left(\mathrm{PO}_{4}\right)_{2}$
(D) $\mathrm{Mg}_{3}\left(\mathrm{PO}_{4}\right)_{2}$
উত্তর : (D) $\mathrm{Mg}_{3}\left(\mathrm{PO}_{4}\right)_{2}$
12. নিম্নের কোন বিক্রিয়াটি ডিসপ্রোপরনেশন বিক্রিয়া ?
(A) $\mathrm{H}_{2} \mathrm{~S}+\mathrm{Cl}_{2} \rightarrow 2 \mathrm{HCl}+\mathrm{S}$
(B) $\mathrm{CuSO}_{4}+\mathrm{NH}_{4} \mathrm{OH} \rightarrow \mathrm{Cu}(\mathrm{OH})_{2}+\left(\mathrm{NH}_{3}\right)_{2} \mathrm{SO}_{4}$
(C) $\mathrm{Fe}+$ dil. $\mathrm{H}_{2} \mathrm{SO}_{4} \rightarrow \mathrm{FeSO}_{4}+\mathrm{H}_{2}$
(D) $\mathrm{Cl}_{2}+\mathrm{NaOH} \rightarrow \mathrm{NaOCl}+\mathrm{NaCl}+\mathrm{H}_{2} \mathrm{O}$
উত্তর : (D) $\mathrm{Cl}_{2}+\mathrm{NaOH} \rightarrow \mathrm{NaOCl}+\mathrm{NaCl}+\mathrm{H}_{2} \mathrm{O}$
13.$18.5 \% \mathrm{~N}_{2} \mathrm{O}_{4}$ $25^{\circ} \mathrm{C}$ তাপমাত্রায় এবং $1 \mathrm{~atm}$ চাপে বিয়োজিত হলে $K_{p}$ এর মান কত ?
(A) $0.142 \mathrm{~atm}$
(B) $0.185 \mathrm{~atm}$
(C) $0.220 \mathrm{~atm}$
(D) $0.125 \mathrm{~atm}$
উত্তর : (A) $0.142 \mathrm{~atm}$
14. নিম্নের মিশ্রণসমূহ থেকে বাফার দ্রবণটি শনাক্ত কর -
(A) $0.2 \mathrm{M}$ $10 \mathrm{~mL}$ $\mathrm{CH}_{3} \mathrm{COOH}+0.2 \mathrm{M}$ $10 \mathrm{~mL}$ $\mathrm{NaOH}$
(B) $0.2 \mathrm{M}$ $10 \mathrm{~mL}$ $\mathrm{CH}_{3} \mathrm{COOH}+0.1 \mathrm{M}$ $10 \mathrm{~mL}$ $\mathrm{NaOH}$
(C) $0.1 \mathrm{M}$ $10 \mathrm{~mL}$ $\mathrm{CH}_{3} \mathrm{COOH}+0.2 \mathrm{M}$ $10 \mathrm{~mL}$ $\mathrm{NaOH}$
(D) $0.2 \mathrm{M}$ $10 \mathrm{~mL}$ $\mathrm{HCl}+0.1 \mathrm{M}$ $10 \mathrm{~mL}$ $\mathrm{NaOH}$
উত্তর : (A) $0.2 \mathrm{M}$ $10 \mathrm{~mL}$ $\mathrm{CH}_{3} \mathrm{COOH}+0.2 \mathrm{M}$ $10 \mathrm{~mL}$ $\mathrm{NaOH}$
15. নিচের কোন যৌগটি Fehling দ্রবণের সাথে বিক্রিয়া করে লাল অধঃক্ষেপ দেয় ?
(A) $\mathrm{RCH}_{2} \mathrm{X}$
(B) $\left(\mathrm{CH}_{3}\right)_{2} \mathrm{CO}$
(C) $\mathrm{RCH}_{2} \mathrm{OH}$
(D) $\mathrm{RCH}_{2} \mathrm{CHO}$
উত্তর : (D) $\mathrm{RCH}_{2} \mathrm{CHO}$
16. একটি $\mathrm{CH}_{3} \mathrm{CN}$ অণুতে $\pi$ এবং $\sigma$ বন্ধনের সংখ্যা যথাক্রমে -
(A) 5 and 2
(B) 4 and 3
(C) 5 and 3
(D) 4 and 2
উত্তর : (A) 5 and 2
17. $\mathrm{IUPAC}$ নামকরণ অনুসারে $\mathrm{CH}_{3}-\mathrm{CH}\left(\mathrm{C}_{2} \mathrm{H}_{2}\right)-\mathrm{CH}_{2}-\mathrm{CHBr}-\mathrm{CHCl}-\mathrm{CH}_{3}$ এর নাম হলো -
(A) 2-chloro-3-bromo-5-ethylhexane
(B) 2-chloro-3-bromo-5-methyl heptane
(C) 3-bromo-2-chloro-5-ethyl-hexane
(D) 3-bromo-2-chloro-5-methyl heptane
উত্তর : (B) 2-chloro-3-bromo-5-methyl heptane
18. নিম্নের কোনটি সবচেয়ে স্থিতিশীল কার্বো-ক্যাটায়ন ?
(A) $\mathrm{CH}_{3}{ }^{+}$
(B) $\left(\mathrm{CH}_{3}\right)_{2} \mathrm{C}^{+} \mathrm{H}$
(C) $\mathrm{H}_{2} \mathrm{C}^{+}-\mathrm{CH}_{3}$
(D) $\left(\mathrm{CH}_{3}\right)_{3} \mathrm{C}^{+}$
উত্তর : (D) $\left(\mathrm{CH}_{3}\right)_{3} \mathrm{C}^{+}$
19. পটাসিয়াম সায়ানাইডের উপস্থিতিতে হাইড্রোজেন সায়ানাইড প্রাপানলের সাথে বিক্রিয়া করে ।বিক্রিয়ার কৌশলটি হলো -
(A) nuclophilic addition
(B) electrophilic substitution
(C) nucleophilic substituton
(D) electrophilic addition
উত্তর : (C) nucleophilic substituton
20. অ্যারোমেটিক প্রতিস্থাপন বিক্রিয়ায় নিম্নের কোন গ্রুপটি মেটা নির্দেশক ?
(A) $-\mathrm{NO}_{3}$
(B) $-\mathrm{OH}$
(C) $-\mathrm{Cl}$
(D) $-\mathrm{CH}_{3}$
উত্তর : (A) $-\mathrm{NO}_{3}$
21. সোডা অ্যাশ শিল্পক্ষেত্রে কোন পদ্ধতিতে তৈরি করা হয় ?
(A) Bessemer process
(B) Chamber process
(C) Solvary process
(D) Haber process
উত্তর : (C) Solvary process
22. এবং অধঃক্ষেপ সমূহের রং-এর ক্রম হলো –
(A)brown, pink, white and blue
(B)brown, blue white and pink
(C)pink, white , brown and blue
(D) brown, white, blue and pink
উত্তর : (B)brown, blue white and pink
23. নিচের কোনটি অসত্য ?
(A) $\mathrm{NH}_{4}^{+}$is the conjugate acid of base $\mathrm{NH}_{3}$
(B) $\mathrm{NH}_{3}$ and $\mathrm{H}_{2} \mathrm{O}$ are conjugate pair
(C) $\mathrm{OH}$ is the conjugate base of acid $\mathrm{H}_{2} \mathrm{O}$
(D) $\mathrm{OH}^{-}$and $\mathrm{H}_{2} \mathrm{O}$ are conjugate pair
উত্তর : (B) $\mathrm{NH}_{3}$ and $\mathrm{H}_{2} \mathrm{O}$ are conjugate pair
24. নিম্নের কোন যৌগটি জলীয় দ্রবণে সবচেয়ে সহজে হাইড্রো-বিশ্লেষিত হয় ?
(A) $\mathrm{CCl}_{4}$
(B) $\mathrm{SnCl}_{2}$
(C) $\mathrm{SiCl}_{4}$
(D) $\mathrm{PbCl}_{4}$
উত্তর : (C) $\mathrm{SiCl}_{4}$
25. নিম্নের কোন যৌগটিতে সঞ্চালন অক্ষম $π$–ইলেক্ট্রন আছ ?
(A) $\mathrm{C}_{2} \mathrm{H}_{6}$
(B) $\mathrm{C}_{6} \mathrm{H}_{6}$
(C) $\mathrm{C}_{3} \mathrm{H}_{8}$
(D) $\mathrm{C}_{2} \mathrm{H}_{4}$
উত্তর : (D) $\mathrm{C}_{2} \mathrm{H}_{4}$
26. $\mathrm{Sr}, \mathrm{Tc}, \mathrm{Zr}$ এবং $\mathrm{Rb}$ পরমানুর ব্যাসার্ধের ক্রম হলো –
(A) $\mathrm{Rb}>\mathrm{Sr}>\mathrm{Zr}>\mathrm{Tc}$
(B) $\mathrm{Tc}>\mathrm{Sr}>\mathrm{Rb}>\mathrm{Zr}$
(C) $\mathrm{Sr}>\mathrm{Tc}>\mathrm{Zr}>\mathrm{Rb}$
(D) $\mathrm{Zr}>\mathrm{Tc}>\mathrm{Rb}>\mathrm{Sr}$
উত্তর : (A) $\mathrm{Rb}>\mathrm{Sr}>\mathrm{Zr}>\mathrm{Tc}$
27. নিম্নের কোন বিক্রিয়াটি প্রশমন এনথালপি, $\Delta H_{\text {neutr }}$ প্রকাশ করে ?
(A) $\mathrm{H}_{2} \mathrm{SO}_{4}$ (aq) $+\mathrm{Ca}(\mathrm{OH})_{2}$ (aq) $\rightarrow \mathrm{CaSO}_{4}$ (aq) $+2 \mathrm{H}_{2} \mathrm{O}$ (l
(B) $\mathrm{H}_{2} \mathrm{SO}_{4}$ (aq) $+2 \mathrm{NH}_{3}$ (aq) $\rightarrow\left(\mathrm{NH}_{4}\right)_{2} \mathrm{SO}_{4}$ (aq)
(C) $\mathrm{HCl}$ (aq) $+1^{1 / 2} \mathrm{Ca}(\mathrm{OH})_{2}$ (aq) $\rightarrow 1 / 2 \mathrm{CaCl}_{2}$ (aq) $+2 \mathrm{H}_{2} \mathrm{O}$ (l)
(D) $2 \mathrm{HCl}$ (aq) $+\mathrm{Ca}$ (OH) $_{2}$ (aq) $\rightarrow \mathrm{CaCl}_{2}$ (aq) $+2 \mathrm{H}_{2} \mathrm{O}$ (l)
উত্তর : (C) $\mathrm{HCl}$ (aq) $+1^{1 / 2} \mathrm{Ca}(\mathrm{OH})_{2}$ (aq) $\rightarrow 1 / 2 \mathrm{CaCl}_{2}$ (aq) $+2 \mathrm{H}_{2} \mathrm{O}$ (l)
28. $\mathrm{Zn}^{+} \mid \mathrm{Zn}$ এবং $\mathrm{Ag}^{+} \mid \mathrm{Ag}$ তড়িৎদ্বার দুটির বিজারণ বিভব যথাক্রমে $-0.76 \mathrm{~V}$ এবং $+0.80 \mathrm{~V}$ এই তড়িৎদ্বার দুটি দ্বারা তৈরি কোষের মোট বিভব কত হবে ?
(A) $-0.04 \mathrm{~V}$
(B) $+1.56 \mathrm{~V}$
(C) +0.14 V
(D) $-1.56 \mathrm{~V}$
উত্তর : (B) $+1.56 \mathrm{~V}$
29.বোল্টজম্যান ধ্রুবকের একক হলো –
(A) J /molecule
(B) J.s
(C) $\mathrm{J} / \mathrm{K}$
(D) g/cc
উত্তর : (A) J /molecule
30. $\operatorname{Sn}(s)+2 \mathrm{Ag}^{+}(\mathrm{aq}) \rightarrow \operatorname{Sn}^{+}(\mathrm{aq})+2 \mathrm{Ag}(\mathrm{s})$ - বিক্রিয়াটির ক্ষেত্রে নিম্নের কোনটি কোষের বৃদ্ধি করবে ?
(A) icrease in the size of silver rod
(B) increase in the concentration of Sn+ ions
(C) increase in the concentration of Ag+ ions
(D) increase in the size of tin rod
উত্তর : (C) increase in the concentration of Ag+ ions
জীববিজ্ঞান
১. বাস্ট তন্ত্র কোনটি ?
ক. পাট তন্ত্র
খ. কার্পাস তন্ত্র
গ. শিমুল তুলা
ঘ. কয়ের
উত্তর : (ক) পাট তন্ত্র
২. মানুষের বক্ষদেশীয় কশেরুকা কয়টি ?
ক. 7
খ. 12
গ. 10
ঘ. 15
উত্তর : খ. 12
৩. কোনটি ommatidium এর অংশ নয় ?
ক. rhabdosome
খ. rentinal sheath
গ. retinal cell
ঘ. ocellus
উত্তর : ঘ. ocellus
৪. গোদরোগ সৃষ্টিকারী পরজীবির নাম-
ক. entamoeba histolytica
খ. Wuchereria bancrofti
গ. Ades fatigans
ঘ. Culex quinquefasciatus
উত্তর : খ. Wuchereria bancrofti
৫. Liliopsida বলতে কি বুঝায়?
ক. একবীজপত্রী উদ্ভিদ
খ. দ্বিবীজপত্রী উদ্ভিদ
গ. লিলিয়েসী গোত্র
ঘ. লিলিয়েলিস বর্গ
উত্তর : ক. একবীজপত্রী উদ্ভিদ
৬. আরশোলার পেরিট্রফিক পর্দা থাকে কোন স্থানে?
ক. ক্রপ
খ. গিজার্ড
গ. হেপাটিক সিকাম
ঘ. মেসেনটিরন
উত্তর : ঘ. মেসেনটিরন
৭. F1-জনুর উদ্ভিদকে প্রচ্ছন্ন প্যারেন্টের সাথে ক্রস করাকে বলা হয়
ক. ব্যাক ক্রস
খ. টেস্ট ক্রস
গ. মনোহাইব্রিড ক্রস
ঘ. ডাইহাইব্রিড ক্রস
উত্তর : খ. টেস্ট ক্রস
৮. মানুষের দেহে কোনটি টেস্টোস্টেরন তৈরি করে?
ক. স্ক্রোটাম
খ. ইন্টারটিস্টিশিয়াল কোষ
গ. ইপিডিডাইমিস
ঘ. স্পারমেটোগোনিয়া
উত্তর : খ. ইন্টারটিস্টিশিয়াল কোষ
৯. ক্রেবস চক্রে কতটি NADH2 তৈরি হয়?
ক. 1
খ. 2
গ. 3
ঘ. 4
উত্তর : গ. 3
১০. কোলারয়েড মূল কোথায় পাওয়া যায়?
ক. Cycas
খ. Ficus
গ. Hibiscus
ঘ. Daucus
উত্তর : ক. Cycas
১১. ইনসুলিন নিঃসরণকারী গ্রন্থির নাম হল-
ক. যকৃত
খ. অগ্ন্যাশয়
গ. প্লীহা
ঘ. আইলেটস অব ল্যাঙ্গারহ্যান্স
উত্তর : ঘ. আইলেটস অব ল্যাঙ্গারহ্যান্স
১২. কোনটি ক্লু মোল্ড?
ক. Penicillium
খ. Saprolegnia
গ. Agaricus
ঘ. Helminthosporium
উত্তর : ক. Penicillium
১৩. অস্থি যে আবরণ দ্বারা আবৃত থাকে তাকে বলে-
ক. পেরিটোনিয়াম
খ. পেরিঅস্টিয়াম
গ. পেরিকার্ডিয়াম
ঘ. পেরিকন্ড্রিয়াম
উত্তর : খ. পেরিঅস্টিয়াম
১৪. ঝিনুকের খোলকের সবচেয়ে ভিতরের স্তরের নাম হল-
ক. ন্যাকার স্তর
খ. প্রিজম্যাটিক স্তর
গ. পেরিওস্ট্রাকাম
ঘ. ম্যান্টল
উত্তর : ক. ন্যাকার স্তর
১৫. নিউক্লিয়াসের প্রথম বর্ণনা করেন-
ক. রবার্ট ব্রাউন
খ. অ্যারিস্টটল
গ. লুই পাস্তুর
ঘ. আলেকজান্ডার ফ্লেমিং
উত্তর : ক. রবার্ট ব্রাউন
১৬. ফুসফুসীয় ধমনী বহন করে-
ক. oxygenetaed blood
খ. deoxygenated blood
গ. pure blood
ঘ. venous blood
উত্তর : খ. deoxygenated blood
১৭. ককলিয়া হল-
ক. দৃষ্টির সাথে সংশ্লিষ্ট অঙ্গ
খ. শ্রবণের সাথে সংশ্লিষ্ট অঙ্গ
গ. ঘ্রাণের সাথে সংশ্লিষ্ট অঙ্গ
ঘ. খাদ্য চর্বণের সাথে সংশ্লিষ্ট অঙ্গ
উত্তর : খ. শ্রবণের সাথে সংশ্লিষ্ট অঙ্গ
১৮. নিচের কোনটি কেবলমাত্র বাংলাদেশে পাওয়া যায়?
ক. Knema bengalensis
খ. Tactaria chattagramica
গ. Artocarpus heterophyllus
ঘ. Ficus benghalensis
উত্তর : ক. Knema bengalensis
১৯. 'Diversity and classification of flowering plants' বইটির লেখক কে?
ক. Carolus Linnaeus
খ. George Bentham
গ. Theophrastus
ঘ. Armen Takhtajan
উত্তর : ঘ. Armen Takhtajan
২০. নিচের কোনটিতে প্লাসমিড নেই?
ক. E. coli
খ. A. Tumefaciens
গ. Yeast
ঘ. Chlorella
উত্তর : গ. Yeast
২১. মানুষের RBC এর গড় আয়ুষ্কাল হচ্ছে-
ক. 96 days
খ. 120 days
গ. 28 days
ঘ. 62 days
উত্তর : খ. 120 days
২২. কোনটি সায়ানোব্যাকটেরিয়া নয়?
ক. Nostoc
খ. Anabaena
গ. Aulosira
ঘ. Clostridium
উত্তর : ঘ. Clostridium
২৩. সপ্তম করোটিকা স্নায়ুকে বলা হয়-
ক. ভেগাস
খ. ট্রক্লিয়ার
গ. ফ্যাসিয়াল
ঘ. অপটিক
উত্তর : গ. ফ্যাসিয়াল
২৪. নিচের কোনটিকে হিল বিক্রিয়া বলা হয়?
ক. CO2 থেকে O2 নির্গমন
খ. H2O থেকে O2 নির্গমন
গ. S2O থেকে O2 নির্গমন
ঘ. NO2 থেকে O2 নির্গমন
উত্তর : খ. H2O থেকে O2 নির্গমন
২৫. ইলেটারের কাজ কী?
ক. খাদ্য তৈরী করা
খ. খাদ্য সঞ্চয় করা
গ. স্পোর নির্গমন সাহায্য করা
ঘ. বংশ বিস্তারে অংশগ্রহণ করা
উত্তর : গ. স্পোর নির্গমন সাহায্য করা
২৬. নিচের কোনটি ফার্ণ পাতার নাম?
ক. Stomium
খ. Fronds
গ. Prothallus
ঘ. Scale leave
উত্তর : খ. Fronds
২৭. মেসোগ্লিয়া পাওয়া যায় কোন প্রাণীতে?
ক. মানুষ
খ. আরশোলা
গ. হাইড্রা
ঘ. মাছ
উত্তর : গ. হাইড্রা
২৮. T2 ব্যাকটেরিওফায়ে কয়টি জীন থাকে?
ক. 150
খ. 145
গ. 155
ঘ. 160
উত্তর :
২৯. ওয়ালেসের লাইন হলো একটি কাল্পনিক সীমারেখা ............ এবং .......... অঞ্চলের মধ্যে অবস্থিত।
ক. ওরিয়েন্ট ও বাংলাদেশ
খ. ইউরোপ ও এশিয়া
গ. বাংলাদেশ ও ভারত
ঘ. কোরিয়া ও জাপান
উত্তর : ক. ওরিয়েন্ট ও বাংলাদেশ
৩০. কোনটি জাইলেম টিস্যুর অংশ নয়?
ক. সিভ নল
খ. ট্র্যাকিড
গ. ট্র্যাকিয়া
ঘ. উড ফাইবার
উত্তর : ক. সিভ নল
English
1. The synonym of 'embellish' is
(A) adorn
(B) shock
(C) impoverish
(D) destroy
Answer: (A) adorn
2. The verb of 'beauty' is
(A) beautician
(B) beautify
(C) beautiful
(D) beautification
Answer: (B) beautify
3. The idiom 'let things slide' means-
(A) ignore
(B) lose gradually
(C) reveal a secret
(D) set free
Answer: (A) ignore
4. Choose the correct spelling
(A) indegenus
(B) indiginous
(C) indigenous
(D) indigeneous
Answer: (C) indigenous
5. Why is the poet so sad to see the daffodils in 'The Daffodils'?
(A) The poet is sad because the flowers have not bloomed fully.
(B) The poet is sad because winter will come soon.
(C) The poet is sad because the flowers remind him of his own death.
(D) The poet is sad because flowers bring very hot weather.
Answer: (C) The poet is sad because the flowers remind him of his own death.
6. The correct translation of ‘রবিবার হইতে বৃষ্টি হইতেছিল’-
(A) It was raining from Sunday.
(B) It has been raining from Sunday.
(C) It had been raining since Sunday.
(D) It rained since Sunday.
Answer: (C) It had been raining since Sunday.
7. The word 'constraint' means
(A) freedom
(B) limitaion
(C) plentiful
(D) endless
Answer: (B) limitaion
8. The expression 'to look after' means
(A) to take care
(B) to follow
(C) to imitate
(D) to gaze
Answer: (A) to take care
9. The antonym of ‘stubborn’ is
(A) agreeable (B) obstinate (C) difficult (D) irritable
Answer: (A) agreeable
10. What is the meaning of the expression “bottom of my heart”?
(A) close to my heart
(B) core of my heart
(C) lower part of my heart
(D) close to my liver
Answer: (B) core of my heart
11. The word ‘desperation’ is a/an
(A) adjective (B) verb (C) adverb (D) noun
Answer: noun
12. Why were the daffodils in Wordswoth’s ‘I Wandered Lonely as a Cloud’ dancing?
(A) The poet was day dreaming.
(B) The flowers had cheerful company.
(C) The sea waves beside them had gone wild.
(D) There was a strong wind.
Answer: (D) There was a strong wind.
Questions 13-22: Fill in the blank/blanks:
13. I’d like ------ information, please.
(A) an
(B) some
(C) few
(D) piece
Answer: (B) some
14. Yoga is ------ a good exercise for ------ breathing.
(A) taken, controlling
(B) treated, considerable
(C) not, slowly
(D) considered, controlling
Answer: (D) considered, controlling
15. A man ----- by a speeding bus while he was crossing the road.
(A) was run over
(B) was run down
(C) had been run
(D) has been run over
Answer: (A) was run over
16. He ----- prefers ----- speak very little.
(A) doesn’t, to
(B) himself, to
(C) himself, for
(D) does, for
Answer: (B) himself, to
17. It ----- heavily when he ----- up.
(A) has snowed, woke
(B) snows, wake
(C) was snowing, woke
(D) is snowing, wakes
Answer: (C) was snowing, woke
18. Misuse of ----- energy has ----- destruction.
(A) solar, shown
(B) renewable, increase
(C) nuclear, cause
(D) atomic, wreaked
Answer: (D) atomic, wreaked
19. There is ----- milk in the bottle.
(A) very few
(B) any
(C) very little
(D) many
Answer: (C) very little
20. I have ------ him to give ----- smoking.
(A) said, up
(B) talked, for
(C) told, up
(D) told, in
Answer: (C) told, up
21. The groom arrived at the community centre exactly ----- time.
(A) in
(B) for
(C) by
(D) on
Answer: (D) on
22. He hates ----- kept ------.
(A) to be, waiting
(B) being kept, wait
(C) to be, to wait
(D) to, waiting
Answer: (A) to be, waiting
Questions 23-25: Choose the correct sentence:
23.
(A) It is you who is to pay.
(B) It is you who are to leave.
(C) It is you who is late.
(D) It is you who has won the prize.
Answer: (B) It is you who are to leave.
24.
(A) He suspicioned that something wrong.
(B) He suspicious that something is wrong.
(C) He suspected that something was wrong.
(D) He suspect that something is wrong.
Answer: (C) He suspected that something was wrong.
25.
(A) The jury are arguing among themselves.
(B) The jury is arguing among themselves.
(C) The jury has argued among themselves.
(D) The jury has been arguing among themselves.
Answer: (A) The jury are arguing among themselves.
Read the passage and answer questions 26-30:
Cats are carnivorous mammals of the family Felidae. They cannot chew their food, and their teeth are adapted to stab, anchor, and cut flesh. All cats except the cheetah have strong, sharp, retractile claws. They are not adapted for long chases but prowl their prey on padded feet and try to overwhelm it in short dash or pounce. Big cats roam over a large area, usually alone but sometimes in family groups, for example, a pride of lions can contain as many as 37 individuals. Cats generally are nocturnal animals, the retina of their eyes made extra sensitive to light by a layer of guanine, which causes the eyes to shine in the dark. Tigers are largest of the cats. They are identified by their characteristic striped coat. They inhabit forests and grasslands in Asia where populations have suffered from haunting, deforestation, and demand for tiger parts in traditional medicine.
26. ‘Cats are nocturnal animals’ means
(A) cats have predatory eyesight
(B) cats are sensitive to smell
(C) cats haunt during daytime
(D) cats are active at night
Answer: (D) cats are active at night
27. A group of lions is called ‘pride of lions’, what is a group of dogs called?
(A) a pack of dogs
(B) a colony of dogs
(C) a flock of dogs
(D) a cluster of dogs
Answer: (A) a pack of dogs
28. ‘retractile claws’ in the passage means
(A) claws the are extra sharp
(B) claws that can change shape
(C) claws that can move inwards
(D) claws that are sensitive to feelings
Answer: (C) claws that can move inwards
29. Cats are carnivorous, but human beings are
(A) herbivorous
(B) omnivorous
(C) farinaceous
(D) cadaverous
Answer: (B) omnivorous
30. The synonym of ‘prowl’ is
(A) dive
(B) chase
(C) ornace
(D) stalk
Answer: (D) stalk
বাংলা
১. পাঞ্জেরী- কবিতায় যাত্রীরা কোথায় বসে অপেক্ষা করে?
ক. তীরে
খ. মাস্তুলে
গ. বন্দরে
ঘ. দাঁড়ে
উত্তর : গ. বন্দরে
টীকা: রাত পোহাবার কত দেরি পাঞ্জেরি?/ বন্দরে বসে যাত্রীরা দিন গোনে, (তৃতীয় স্তবক)
২. নিচের কোনটি শুদ্ধ বানান?
ক. স্বায়ত্ত্বশাসন
খ. সায়ত্ত্বশাসন
গ. স্বায়ত্তশাসন
ঘ. স্বায়ত্ত্বশাষণ
উত্তর : গ. স্বায়ত্তশাসন
৩. বিলাসী- গল্পে উনিশ শতকের যে সমাজ-সংস্কারের কথা আছে তাঁর নাম-
ক. ঈশ্বরচন্দ্র বিদ্যাসাগর
খ. রামমোহন রায়
গ. অক্ষয়কুমার দত্ত
ঘ. ভূদেব মুখোপাধ্যায়
উত্তর : ঘ. ভূদেব মুখোপাধ্যায়
টীকা: আমি ভূদেববাবুর পারিবারিক প্রবন্ধেরও দোষ দিব না এবং শাস্ত্রীয় বিধি-ব্যবস্থারও নিন্দা করিব না। (শেষ অনুচ্ছেদ/প্যারাগ্রাফ)
৪. সন্ধিঘটিত কোন শব্দটি শুদ্ধ?
ক. বৃহদংশ
খ. জাত্যাভিমান
গ. আদ্যান্ত
ঘ. শিরোচ্ছেদ
উত্তর : ক. বৃহদংশ
৫. তাম্রশাসন- মানে?
ক. স্বৈরশাসন
খ. কালো আইন
গ. তামার পাতে খোদাই করা আদেশ
ঘ. একজন রাজার নাম
উত্তর : গ. তামার পাতে খোদাই করা আদেশ
৬. দেহের বয়স অনুযায়ী মনের বয়স না বাড়লে তাকে বলে-
ক. শারীরিক প্রতিবন্ধী
খ. মনোবিকারগ্রস্ত
গ. মানসিক রোগী
ঘ. বুদ্ধিপ্রতিবন্ধী
উত্তর : ঘ. বুদ্ধিপ্রতিবন্ধী
৭. কোন শব্দটি শুদ্ধ?
ক. সমীক্ষন
খ. সমীচীন
গ. শিরচ্ছেদ
ঘ. ভাষ্কর
উত্তর : খ. সমীচীন
৮. মাতৃহৃদয়ে পক্ষপাতিতা নাই।– বাক্যটি কোন রচনার অন্তর্গত?
ক. অর্ধাঙ্গী
খ. যৌবনের গান
গ. বিলাসী
ঘ. কমলাকান্তের দপ্তর
উত্তর : ক. অর্ধাঙ্গী
৯. বাংলা ব্যঞ্জনবর্ণের প্রতিবর্গের পঞ্চম বর্গের ধ্বনিটি-
ক. ঘোষধ্বনি
খ. অঘোষধ্বনি
গ. মহাপ্রাণধ্বনি
ঘ. নাসিক্যধ্বনি
উত্তর : ঘ. নাসিক্যধ্বনি
লিঙ্ক: ধ্বনি ও বর্ণ প্রকরণ ও উচ্চারণবিধি
১০. যেমন কর্ম তেমন ফল- এ বাক্যে ব্যবহৃত হয়েছে-
ক. নির্ধারক বিশেষণ
খ. ক্রিয়া বিশেষণ
গ. সাপেক্ষ সর্বনাম
ঘ. বিশেষণের বিশেষণ
উত্তর : গ. সাপেক্ষ সর্বনাম
লিঙ্ক: পদ প্রকরণ
১১. প্রমথ চৌধুরী সম্পাদিত সবুজপত্র- পত্রিকা কত সালে প্রকাশিত হয়?
ক. ১৯১৩
খ. ১৯১৪
গ. ১৯১৫
ঘ. ১৯১৭
উত্তর : খ. ১৯১৪
১২. ঊর্ণাজাল- শব্দের অর্থ
ক. দোপাট্টা
খ. কুজ্ঝটিকা
গ. মাকড়সাল তৈরি জাল
ঘ. মাছধরার নিক্ষেপযোগ্য জাল
উত্তর : গ. মাকড়সাল তৈরি জাল
১৩. পাঠ্য কোন কবিতায় বাতাবি নেবু-র উল্লেখ আছে?
ক. তাহারেই পড়ে মনে
খ. বাংলাদেশ
গ. একটি ফটোগ্রাফ
ঘ. কবর
উত্তর : ক. তাহারেই পড়ে মনে
টীকা: বাতাবি নেবুর ফুল ফুটেছে কি? ফুটেছে কি আমের মুকুল? (প্রথম স্তবক)
১৪. একাধিক স্বাধীন বাক্যকে একটি বাক্যে লিখলে সেগুলোর মাঝখানে কী চিহ্ন ব্যবহৃত হয়?
ক. কোলন
খ. ড্যাশ
গ. সেমিকোলন
ঘ. কমা
উত্তর : ঘ. কমা
১৫. আমাদের দলে কেহ দলপতি নাই।- কাহাদের দলে?
ক. কবিদের
খ. তরুণদের
গ. সাধকদের
ঘ. বক্তাদের
উত্তর : খ. তরুণদের
টীকা: আমাদের দলে কেহ দলপতি নাই, আজ আমরা শত দিক হইতে শত শত তরুণ মিলিয়া তারুণ্যের শতদল ফুটাইয়া তুলিয়াছি। (চতুর্থ অনুচ্ছেদ)
১৬. The situation has come to a head- এর অর্থ-
ক. পরিস্থিতির উন্নতি ঘটেছে
খ. পরিস্থিতি সবচেয়ে ভালো অবস্থায় এসে দাঁড়িয়েছে
গ. পরিস্থিতির অবনতি ঘটেছে
ঘ. পরিস্থিতি চরম অবস্থায় পৌঁছেছে
উত্তর : ঘ. পরিস্থিতি চরম অবস্থায় পৌঁছেছে
১৭. মণ্ডক- শব্দের অর্থ-
ক. মুণ্ডধারী
খ. ভেক
গ. কুয়ো
ঘ. মিষ্টিজাতীয় দ্রব্য
উত্তর : খ. ভেক
১৮. নিচের কোনটি শামসুর রাহমানের কাব্যগ্রন্থ নয়?
ক. দুঃসময়ের মুখোমুখি
খ. উদ্ভট উটের পিঠে চলেছে স্বদেশ
গ. নিজ বাসভূমে
ঘ. একক সন্ধ্যায় বসন্ত
উত্তর : ঘ. একক সন্ধ্যায় বসন্ত
১৯. কোন শব্দটি উপসর্গযোগে গঠিত?
ক. অবরেণ্য
খ. তরুণ
গ. পরীক্ষা
ঘ. কলুষ
উত্তর : ক. অবরেণ্য
লিঙ্ক: উপসর্গ
২০. সাহচর্য- শব্দটি গঠিত হয়েছে
ক. প্রত্যয়যোগে
খ. ধাতুযোগে
গ. সন্ধিযোগে
ঘ. সমাসযোগে
উত্তর : ক. প্রত্যয়যোগে
লিঙ্ক: প্রকৃতি-প্রত্যয়
২১. নিরাকার- শব্দের সন্ধিবিচ্ছেদ কোনটি?
ক. নি+আকার
খ. নিঃ+আকার
গ. নির+আকার
ঘ. নিরঃ+আকার
উত্তর : খ. নিঃ+আকার
২২. কর্বূর- শব্দের অর্থ
ক. রাক্ষস
খ. গন্ধদ্রব্যবিশেষ
গ. রাসায়নিক পদার্থ
ঘ. করণীয়
উত্তর : ক. রাক্ষস
২৩. তুষারধবল- কোন সমাসের উদাহরণ?
ক. সাধারণ কর্মধারয়
খ. উপমান কর্মধারয়
গ. উপমিত কর্মধারয়
ঘ. মধ্যপদলোপী কর্মধারয়
উত্তর : খ. উপমান কর্মধারয়
লিঙ্ক: সমাস
২৪. ণ-ত্ব বিধি অনুসারে কোন গুচ্ছ অশুদ্ধ বানানের দৃষ্টান্ত?
ক. ধরন, বরণ
খ. বর্ননা, পুরোনো
গ. নেত্রকোনা, পরগনা
ঘ. রূপায়ণ, প্রণয়ন
টীকা: দ্বিতীয় গুচ্ছের শুদ্ধরূপ- বর্ণনা, পুরনো
উত্তর : খ. বর্ননা, পুরোনো
লিঙ্ক: ণত্ব ও ষত্ব বিধান
২৫. সমভিব্যাহার- শব্দটিতে মোট কয়টি উপসর্গ আছে?
ক. ২
খ. ৩
গ. ১
ঘ. ৪
টীকা: সম+অভি+বি+হার (সম, অভি, বি- ৩টি উপসর্গ)
উত্তর : খ. ৩
লিঙ্ক: উপসর্গ
২৬. কাব্য জগতে যার নাম আনন্দ তারেই নাম বেদনা।– বাক্যটি আছে যে রচনায়-
ক. বিলাসী
খ. হৈমন্তী
গ. সাহিত্যে খেলা
ঘ. যৌবনের গান
উত্তর : গ. সাহিত্যে খেলা
২৭. কার মেছোয়াক করা দাঁত বালব-এর আলোয় ঝকঝক করে?
ক. মোদাব্বেরের
খ. মকসুদের
গ. ইউনুসের
ঘ. রাহাতের
উত্তর : ক. মোদাব্বেরের
টীকা: -ওরাই তো সবকিছুর মূলে, মোদাব্বের বলে। উলঙ্গ বালব-এর আলোয় তার সযত্নে মেছোয়াক করা দাঁত ঝকঝক করে। তাদের নীচতা হীনতা গোঁড়ামির জন্যেই তো দেশটা ভাগ হলো।
২৮. Lyric শব্দের বাংলা পরিভাষা=
ক. গান
খ. সুর
গ. কথা
ঘ. গীতিকবিতা
উত্তর : ঘ. গীতিকবিতা
২৯. Vertical শব্দের পরিভাষা-
ক. অনুভূমিক
খ. উচ্চতা
গ. উল্লম্ব
ঘ. দেয়াল
উত্তর : গ. উল্লম্ব
৩০. পিপাসিত শব্দের বিশেষ্যরূপ-
ক. পিপাসী
খ. পিপাসু
গ. পিপাসা
ঘ. পিয়াসী
উত্তর : গ. পিপাসা

বাংলা ১৭ নং এর উত্তর কোনটি ?
বাংলা ১৭ নং এর উত্তর কোনটি ?
physics
5 & 11 no ans are incorrect.....5(গ) & 11 (ক)
physics
vaia sound diffraction show kre bt plarisation shoe kre na........source shajahan tapan sir er boi.......
boltsman's constant er akok J/K (source phy 1,tofajjol sir)
r hidrogen poromanur shoktistor er ans to 10.2ev hoar kotha,as energy absorvation E=E2-E1?
ENGLISH 25 No. er ans Wrong!!
25.
(A) The jury are arguing among themselves.
(B) The jury is arguing among themselves.
(C) The jury has argued among themselves.
(D) The jury has been arguing among themselves.
Answer: (B) The jury is arguing among themselves.
Jury er por is boshe.MS word a dilei correct kore dibe.
Physics
Ans. A
গণিত এর ২৭ নং প্রশ্নের উত্তর
গণিত এর ২৭ নং প্রশ্নের উত্তর ভুল রয়েছে । প্রশ্নে একটি মোজা পরার কথা বলা হয়েছে । কিন্তু এই সমাধানে এক জোরা মোজা হিসাব করা হয়েছে ।
chemistry
chemistry 17 number question er ans b hobe.
12.গ) 10.2eV 13.6-3.4=10.2 eV
12.গ) 10.2eV
13.6-3.4=10.2 eV
20. 50/20=2.5
20. 50/20=2.5
biology
bio 8 num ki thik ace????
13. I’d like ------
13. I’d like ------ information, please.
(A) an
(B) some
(C) few
(D) piece
এটা তো মনে হয় Few হয়ার কথা। আমার জানা মতে Information এর আগে Few বসে।
১ নং প্রশ্ন (physics)
১ নং প্রশ্নের ব্যাখ্যায় ভুল রয়েছে ৷
MATH আর PHYSICS সঠিক উত্তরের
MATH আর PHYSICS সঠিক উত্তরের পাশাপাশি সমাধান দিয়ে দেওয়াতে ধন্যবাদ!!
chemistry
২৯ নং প্রশ্নের উত্তর C J/k
ফিজিক্স
tnx a lot
নতুন কমেন্ট যুক্ত করুন