কোণের ডিগ্রী ও রেডিয়ান পরিমাপের সম্পর্ক
1° = $\frac{\pi}{180}$ রেডিয়ান
1 রেডিয়ান = $\frac{180^{\circ}}{\pi}$
লক্ষণীয়, π ≈ 3.1416 … …. এবং πc = π রেডিয়ান = 180°
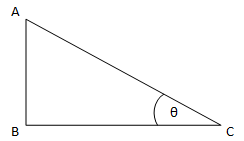
সূক্ষ্মকোণের ত্রিকোণমিতিক অনুপাত: মনে করি, ABC সমকোণী ত্রিভুজে ∠ABC = এক সমকোণ এবং ∠ACB = θ। তাহলে,
অতিভুজ = সমকোণের বিপরীত বাহু = AC
লম্ব = θ কোণের বিপরীত বাহু = AB
ভূমি = অতিভুজ ব্যতীত θ কোণের সন্নিহিত অপর বাহু = BC
∴ θ সূক্ষ্মকোণের ত্রিকোণমিতিক অনুপাতগুলো হল,
sin θ = লম্ব / অতিভুজ = $\frac{A B}{A C}=\frac{1}{\operatorname{cosec} \theta}$
cosec θ = অতিভুজ / লম্ব = $\frac{A C}{A B}=\frac{1}{\sin \theta}$
cos θ = ভূমি / অতিভুজ = $\frac{B C}{A C}=\frac{1}{\sec \theta}$
sec θ = অতিভুজ / ভূমি = $\frac{A C}{B C}=\frac{1}{\cos \theta}$
tan θ = লম্ব / ভূমি = $\frac{A B}{B C}=\frac{1}{\cot \theta}=\frac{\sin \theta}{\cos \theta}$
cot θ = ভূমি / লম্ব = $\frac{B C}{A B}=\frac{1}{\tan \theta}=\frac{\cos \theta}{\sin \theta}$
যেকোনো সাধারণ কোণের ত্রিকোণমিতিক অনুপাত: মনে করি, X′OX রেখা x অক্ষ, YOY′ রেখা y অক্ষ এবং O মূলবিন্দু। এখানে, ধনাত্মক x অক্ষ অর্থাৎ OX রশ্মি থেকে ঘড়ির কাঁটার বিপরীত দিকে ঘূর্ণনের ফলে ∠XOP = θ কোণের সৃষ্টি হয়েছে যেখানে OX কোণটির আদি বাহু (initial side) এবং OP প্রান্তিক বাহু (terminal side)। P(x,y) বিন্দুর অবস্থান XOY, X′OY, X′OY′ অথবা Y′OX এই চারটি চতুর্ভাগের (quadrant) যেকোনো একটিতে হতে পারে।
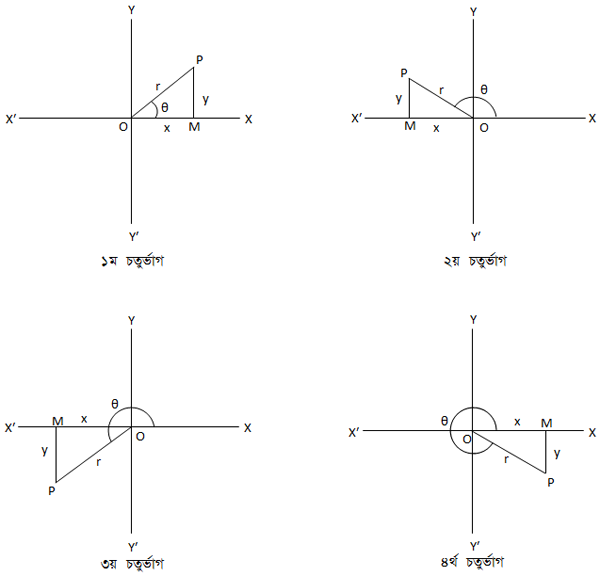
P বিন্দু থেকে XOX′ রেখার উপর PM লম্ব আকা হল। মূলবিন্দু O থেকে P বিন্দুর দূরত্ব OP কে P বিন্দুর ব্যাসার্ধ ভেক্টর। এখানে,
OP = ব্যাসার্ধ ভেক্টর = অতিভুজ = r
PM = x অক্ষ থেকে P বিন্দুর দূরত্ব = লম্ব = y
OM = y অক্ষ থেকে P বিন্দুর দূরত্ব = ভূমি = x
∴ θ কোণের ত্রিকোণমিতিক অনুপাতগুলো নিম্নরূপ:
$\sin \theta=\frac{\mathrm{pM}}{\mathrm{OP}}=\frac{\mathrm{y}}{\mathrm{r}}$
$\operatorname{cosec} \theta=\frac{\text { OP }}{\mathrm{pM}}=\frac{\mathrm{r}}{\mathrm{y}}$
$\cos \theta=\frac{\mathrm{OM}}{\mathrm{OP}}=\frac{\mathrm{x}}{\mathrm{r}}$
$\sec \theta=\frac{O \mathrm{P}}{O \mathrm{M}}=\frac{\mathrm{r}}{\mathrm{x}}$
$\tan \theta=\frac{\mathrm{PM}}{\mathrm{OM}}=\frac{\mathrm{y}}{\mathrm{x}}$
$\cot \theta=\frac{\mathrm{OM}}{\mathrm{PM}}=\frac{\mathrm{x}}{\mathrm{y}}$
‒ θ (0° < θ < 90°) কোণের ত্রিকোণমিতিক অনুপাত: ধনাত্মক x অক্ষ অর্থাৎ OX রশ্মি থেকে ঘড়ির কাঁটার দিকে ঘূর্ণনের ফলে ঋণাত্মক θ কোণ সৃষ্টি হয়।
sin (‒ θ) = ‒ sin θ
cosec (‒ θ) = ‒ cosec θ
tan (‒ θ) = ‒ tan θ
cot (‒ θ) = ‒ cot θ
cos (‒ θ) = cos θ
sec (‒ θ) = sec θ
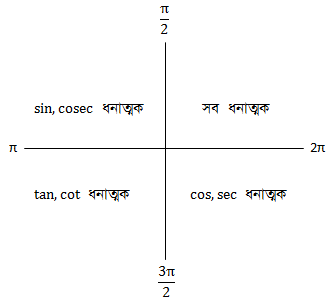
ত্রিকোণমিতিক অনুপাতের চিহ্ন: θ ধনাত্মক বা ঋণাত্মক যা-ই হোক না কেন, θ কোণের ত্রিকোণমিতিক অনুপাতগুলোর মান ধনাত্মক বা ঋণাত্মক হয় P এর অবস্থান তথা θ কোণের প্রান্তিক বাহুর অবস্থানের উপর ভিত্তি করে। ১ম চতুর্ভাগে সব অনুপাতই ধনাত্মক। ২য় চতুর্ভাগে sine ও cosec ধনাত্মক, বাকিগুলো ঋণাত্মক। ৩য় চতুর্ভাগে tangent ও cotangent ধনাত্মক, বাকিগুলো ঋণাত্মক। ৪র্থ চতুর্ভাগে cosine ও secant ধনাত্মক, বাকিগুলো ঋণাত্মক।
মৌলিক ত্রিকোণমিতিক সূত্র: sin2 θ + cos2 θ = 1
sec2 θ = 1 + tan2 θ
cosec2 θ = 1 + cot2 θ
ত্রিকোণমিতিক অনুপাতের সীমাবদ্ধতা: ‒ 1 ≤ sin θ ≤ 1
‒ 1 ≤ cos θ ≤ 1
sec θ ≥ 1 or sec θ ≤ ‒ 1
cosec θ ≥ 1 or cosec θ ≤ ‒ 1
0°, 30°, 45°, 60° ও 90° কোণের ত্রিকোণমিতিক অনুপাতগুলোর মান:
ত্রিকোণমিতিক অনুপাতে কোণগুলো যখন π এর গুণিতক বা উপগুণিতক হিসেবে দেওয়া থাকে তখন অনুপাতগুলো মূলত রেডিয়ান কোণের ত্রিকোণমিতিক অনুপাত প্রকাশ করে থাকে। অর্থাৎ,
$\sin \frac{\pi}{3} \neq \sin \frac{3.14159 \ldots \ldots}{3}$ বরং, $\sin \frac{\pi}{3}=\sin \frac{\pi^{c}}{3}=\sin \frac{180^{\circ}}{3}=\sin 60^{\circ}$ [কোণের ডিগ্রী ও রেডিয়ান পরিমাপের সম্পর্ক দ্রষ্টব্য]
|
0° |
30° |
45° |
60° |
90° |
|
|
sine |
0 |
1 |
|||
|
cosine |
1 |
0 |
|||
|
tangent |
0 |
1 |
অসংজ্ঞায়িত |
||
|
cotangent |
অসংজ্ঞায়িত |
1 |
0 |
||
|
secant |
1 |
2 |
অসংজ্ঞায়িত |
||
|
cosecant |
অসংজ্ঞায়িত |
2 |
1 |
