সরলরেখা (Straight Lines)

সাধারণ ধারণা

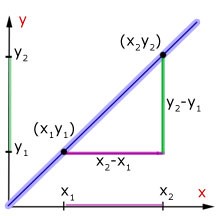
1.  A (x₁,y₁) ও B (x₂,y₂) বিন্দুগামী সরলরেখার ঢাল(gradient) ,

m = কোটিদ্বয়ের অন্তর / ভুজদ্বয়ের অন্তর = $\frac{y_{1}-y_{2}}{x_{1}-x_{2}}$     

 

2. ax+by+c=0 সরলরেখার ঢাল, m = -(a/b)

3. A (x₁, y₁), B (x₂, y₂) এবং C (x₃, y₃) বিন্দু তিনটি সমরেখ হবে যদি AB এবং AC রেখাদ্বয়ের ঢাল একই হয় ।

 

অর্থাৎ যদি, $\frac{y_{1}-y_{2}}{x_{1}-x_{2}}=\frac{y_{1}-y_{3}}{x_{1}-x_{3}}$ হয়

4. x অক্ষের সমীকরণ, y = 0

5. y অক্ষের সমীকরণ, x = 0

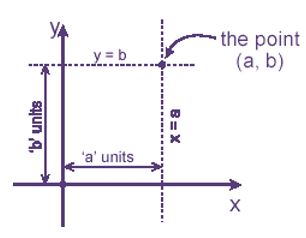
6. x অক্ষের সমান্তরাল সরলরেখার সমীকরণ, y = b                                                                                               

7. y অক্ষের সমান্তরাল সরলরেখার সমীকরণ, x = a

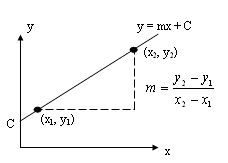
8. y অক্ষ থেকে নিদিষ্ট অংশ c ছেদ করে এবং x অক্ষের সাথে ধনাত্মক কোণ θ উৎপন্ন করে এরূপ সরলরেখার সমীকরণ, y = mx+c

এখানে, m = সরলরেখার ঢাল = tanθ

                                               

c = 0 হলে সরলরেখাটি মূলবিন্দুগামী হয় এবং সমীকরণটি দাড়ায়, y = mx

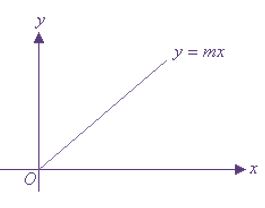
9.(x₁,y₁) বিন্দুগামী m ঢাল বিশিষ্ট সরলরেখার সমীকরণ
y-y₁ = m(x-x₁)

10.(x₁, y₁) ও (x₂,y₂) বিন্দুগামী এবং y অক্ষের সমান্তরাল নয় এরূপ রেখার সমীকরণ,
$\frac{x-x_{1}}{x_{1}-x_{2}}=\frac{y-y_{1}}{y_{1}-y_{2}}$

11.মূলবিন্দু (0,0) এবং (x₁,y₁) বিন্দুর সংযোগকারী সরলরেখার সমীকরণ,
(x/x₁) = (y/y₁)

12.x অক্ষ থেকে নির্দিষ্ট অংশ a এবং y অক্ষ থেকে নির্দিষ্ট অংশ b ছেদ করে এরূপ সরলরেখার সমীকরণ, x/a + y/b = 1

    সরলরেখাটি x অক্ষরেখাকে (a,0) এবং y অক্ষরেখাকে (0,b) বিন্দুতে ছেদ করে

13. মূলবিন্দু থেকে যে সরলরেখার উপর অঙ্কিত লম্ব x অক্ষের ধনাত্মক দিকের সাথে Θ কোণ উৎপন্ন করে এবং যার উপর মূলবিন্দু থেকে অঙ্কিত লম্বের দৈর্ঘ্য p তার সমীকরণ, x cosθθ + ysinθθ = p

14. দুইটি সরলরেখার সমীকরণ সমাধান করলে তাদের ছেদবিন্দুর স্থানাঙ্ক পাওয়া যায় ।

15. a₁x+b₁y+c₁ = 0 এবং a₂x+b₂y+c₂ = 0 সরলরেখাদ্বয়ের ছেদবিন্দুগামী সরলরেখার সমীকরণ,
a₁x+b₁y+c₁+k(a₂x+b₂y+c₂) = 0

k-এর বিভিন্ন মানের জন্য সমীকরণটি বিভিন্ন সরলরেখা প্রকাশ করে যার প্রত্যেকেই উক্ত ছেদ বিন্দুগামী ।

16. (x₁, y₁) ও (x₂,y₂) বিন্দুদ্বয় ax+by+c = 0 রেখার একই পার্শ্বে অবস্থিত হবে যদি a₁x+b₁y+c এবং a₂x+b₂y+c রাশিদ্বয় একই চিহ্নবিশিষ্ট হয় ।

17. (x₁, y₁) ও (x₂,y₂) বিন্দুদ্বয় ax+by+c = 0 রেখার বিপরীত পার্শ্বে অবস্থিত হবে যদি a₁x+b₁y+c এবং a₂x+b₂y+c রাশিদ্বয় বিপরীত চিহ্ন বিশিষ্ট হয় ।

18. দুইটি সরলরেখার ঢাল যথাক্রমে m₁ ও m₂ হলে তারা পরস্পর লম্ব হবে যদি m₁×m₂ = -1 হয় এবং তারা পরস্পর সমান্তরাল হবে যদি m₁= m₂ হয় ।

19. a₁x+b₁y+c₁ = 0 এবং a₂x+b₂y+c₂ = 0 রেখাদ্বয় পরস্পর লম্ব হবে যদি a₁a₂+b₁b₂ = 0 হয় এবং তারা পরস্পর সমান্তরাল হবে যদি (a₁/b₁) = (a₂/b₂) হয় ।

20. দুইটি সরলরেখার ঢাল যথাক্রমে m₁ ও m₂ এবং তাদের মধ্যবর্তী/অন্তর্ভুক্ত কোণ θ হলে,

$\tan \theta=\pm \frac{m_{1}-m_{2}}{1+m_{1} m_{2}}$

tanθ এর ধনাত্মক মান অন্তর্ভুক্ত সূক্ষ্মকোণ এবং ঋণাত্মক মান অন্তর্ভুক্ত স্থূল কোণ নির্দেশ করে ।

21. a₁x+b₁y+c₁ = 0 এবং a₂x+b₂y+c₂ = 0 এবং রেখাদ্বয়ের অন্তর্ভুক্ত কোণ θ হলে,

$\tan \theta=\pm \frac{a_{1} b_{2}-b_{1} a_{2}}{a_{1} a_{2}+b_{1} b_{2}}$

tanθ এর ধনাত্মক মান অন্তর্ভুক্ত সূক্ষ্মকোণ এবং ঋণাত্মক মান অন্তর্ভুক্ত স্থূল কোণ নির্দেশ করে ।

22. ax+by+c1 = 0 রেখার সমান্তরাল কোনো রেখার সমীকরণ হবে, ax+by+c2 = 0 অর্থাৎ,শুধু ধ্রুবক পদটির পরিবর্তন হবে ।

23. (x1,y1) বিন্দুগামী এবং ax+by+c = 0 রেখার সমান্তরাল রেখার সমীকরণ, a(x-x1)+b(y-y1) = 0

24. ax+by+c₁ = 0 রেখার লম্ব কোনো রেখার সমীকরণ হবে, bx-ay+c₂ = 0 অর্থাৎ, x ও y এর সহগদ্বয় পরস্পর স্থান পরিবর্তন করবে, এদের একটির চিহ্ন পরিবর্তিত হবে এবং ধ্রুবক পদটি পরিবর্তিত হবে ।

25. (x₁,y₁) বিন্দুগামী এবং ax+by+c = 0 রেখার লম্ব রেখার সমীকরণ, b(x-x₁) – a(y-y₁) = 0

26. a₁x+b₁y+c₁ = 0; a₂x+b₂y+c₂ = 0 এবং a₃x+b₃y+c₃ = 0  রেখাত্রয় সমবিন্দু হবে যদি,

 

$\left|\begin{array}{lll}a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3}\end{array}\right|=0$ হয় ।

 

 27. উক্ত রেখাত্রয় দ্বারা গঠিত ত্রিভুজ ক্ষেত্রের ক্ষেত্রফল = $\frac{\mathrm{D}^{2}}{2 \mathrm{C}_{1} \mathrm{C}_{2} \mathrm{C}_{3}}$

যেখানে, $\mathrm{D}=\left|\begin{array}{lll}\mathrm{a}_{1} & \mathrm{~b}_{1} & \mathrm{c}_{1} \\ \mathrm{a}_{2} & \mathrm{~b}_{2} & \mathrm{c}_{2} \\ \mathrm{a}_{3} & \mathrm{~b}_{3} & \mathrm{c}_{3}\end{array}\right|$  এবং C₁, C₂, C₃ যথাক্রমে c₁, c₂, c₃ এর সহগুণক ।

 

28. ax+by+c = 0 সরলরেখা থেকে (x1,y1) বিন্দুর লম্ব দূরত্ব,

$\mathrm{d}=\frac{\left|a x_{1}+b y_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}$

29. দুইটি সমান্তরাল রেখা ax+by+c₁ = 0 ও ax+by+c₂ = 0 এর মধ্যবর্তী দূরত্ব, $\mathrm{d}=\frac{\left|c_{1}-c_{2}\right|}{\sqrt{a^{2}+b^{2}}}$

30. a₁x+b₁y+c₁ = 0 এবং a₂x+b₂y+c₂ = 0 রেখাদ্বয়ের অন্তর্ভুক্ত কোণের সমদ্বিখণ্ডক সরলরেখাদ্বয়ের সমীকরণ,

$\frac{a_{1} x+b_{1} y+c_{1}}{\sqrt{a_{1}^{2}+b_{1}^{2}}}=\pm \frac{a_{2} x+b_{2} y+c_{2}}{\sqrt{a_{2}^{2}+b_{2}^{2}}}$

1. a₁a₂+b₁b₂ > 0 হলে + চিহ্নধারী সমীকরণটি স্থূলকোণের এবং - চিহ্নধারী সমীকরণটি সূক্ষ্মকোণের সমদ্বিখণ্ডক নির্দেশ করে ।
2. a₁a₂+b₁b₂ < 0 হলে + চিহ্নধারী সমীকরণটি সূক্ষ্মকোণের এবং – চিহ্নধারী সমীকরণটি স্থূলকোণের সমদ্বিখণ্ডক নির্দেশ করে ।

 

গাণিতিক সমস্যার উদাহরণ ও সমাধান 

 

1. (-1,3) ও (4,-2) বিন্দুগামী সরলরেখার অক্ষদ্বয়ের মধ্যবর্তী খণ্ডিত অংশটুকুর দৈর্ঘ্য কত ?

 

সমাধানঃ

উক্ত বিন্দুগামী সরলরেখার সমীকরণ,
$\frac{x+1}{-1-4}=\frac{y-3}{3+2}$   [(x₁, y₁) ও (x₂,y₂) বিন্দুগামী সরলরেখার সমীকরণ, $\frac{x-x_{1}}{x_{1}-x_{2}}=\frac{y-y_{1}}{y_{1}-y_{2}}$ ]
⇒ $\frac{x+1}{-5}=\frac{y-3}{5}$
⇒ x+1 = -y+3
⇒ x+y = 2
⇒ x/2 + y/2 = 0    [x/a + y/b = 1 সরলরেখা x অক্ষকে (a,0) ও y অক্ষকে (0,b) বিন্দুতে ছেদ করে]
∴ সরলরেখাটি x অক্ষকে (2,0) এবং y অক্ষকে (0,2) বিন্দুতে ছেদ করে ।

∴ অক্ষদ্বয়ের মধ্যবর্তী খণ্ডিত অংশ = $\sqrt{(2-0)^{2}+(0-2)^{2}}$       

[(x₁,y₁) ও (x₂,y₂) বিন্দুদ্বয়ের মধ্যবর্তী দূরত্ব = $\sqrt{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}}$ ]
= √8
= 2√2  [ans.]

2. এমন একটি সরলরেখার সমীকরণ নির্ণয় কর যা (3,2) বিন্দু দিয়ে অতিক্রম করে এবং x ও y অক্ষকে যথাক্রমে A ও B বিন্দুতে ছেদ করে। যেন OA-OB = 2 হয়, যখন O মূলবিন্দু।

 

সমাধানঃ

ধরি, সরলরেখাটির সমীকরণ, x/a + y/b = 1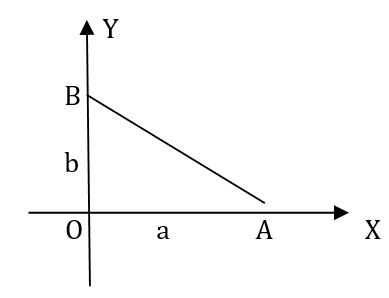                           
সরলরেখাটি (3,2) বিন্দুগামী ।           
∴ 3/a + 2/b = 1                                        
⇒ 3b+2a = ab  ...(i)                                 
আবার, OA-OB = 2
⇒ a-b = 2
⇒ a = 2+b
∴ (i) ⇒ 3b+2(2+b) = (2+b)b
⇒ b²-3ab-4 = 0
⇒ b = 4, -1
যখন, b = 4 তখন, a = 6
∴ x/6 + y/4 = 1
⇒ 2x+3y = 12   [ans.]
যখন, b = -1 তখন, a = 1
∴ x/1 + y/-1 = 1
⇒ x-y  = 1    [ans.]

 

3. ax+by = c এবং x cosα + y sinα = p একই সরলরেখা নির্দেশ করলে p এর মান a,b তে প্রকাশ কর ।

সমাধানঃ

∴ $\frac{a}{\cos \alpha}=\frac{b}{\sin \alpha}=\frac{c}{p}$

⇒ $\frac{a^{2}}{\cos ^{2} \alpha}=\frac{b^{2}}{\sin ^{2} \alpha}=\frac{c^{2}}{p^{2}}$

⇒ $\frac{c^{2}}{p^{2}}=\frac{a^{2}+b^{2}}{\cos ^{2} \alpha+\sin ^{2} \alpha}$

⇒ $\frac{c^{2}}{p^{2}}=\mathrm{a}^{2}+\mathrm{b}^{2}$

⇒ $\mathrm{p}^{2}=\frac{c^{2}}{a^{2}+b^{2}}$

∴ $\mathrm{p}=\pm \frac{c}{\sqrt{a^{2}+b^{2}}}$              [answer]

 

4. একটি সরলরেখা অক্ষ দুইটি থেকে সমমানের যোগবোধক অংশ ছেদ করে । মূলবিন্দু থেকে তার উপর অঙ্কিত লম্বের দৈর্ঘ্য 4 একক । তার সমীকরণ বের কর ।

 

সমাধানঃ

সরলরেখাটি অক্ষ দুইটি থেকে সমমানের যোগবোধক a অংশ ছেদ করলে,
সরলরেখার সমীকরণ, x/a + y/a = 1
⇒ x+y = a ...(i)
আবার, মূলবিন্দু থেকে সরলরেখাটির উপর অঙ্কিত লম্ব যদি x অক্ষের ধনাত্মক দিকের সাথে α কোণ উৎপন্ন করে তবে,
সরলরেখাটির সমীকরণ, x cosα + y sinα = 4
∵ (i) ও (ii) একই সরলরেখা নির্দেশ করে
∴ 1/cosα = 1/sinα = a/4
⇒ $\frac{1}{\cos ^{2}}=\frac{1}{\sin ^{2}}=\frac{a^{2}}{16}$
⇒ $\frac{a^{2}}{16}=\frac{1+1}{\cos ^{2}+\sin ^{2}}$
⇒ a² = 16×2
⇒ a = 4√2       [answer]

 

5. k এর সব মানের জন্য একগুচ্ছ সরলরেখা (3+2k)x+5ky-3 = 0 একটি নির্দিষ্ট বিন্দুগামী। বিন্দুটির স্থানাংক নির্ণয় কর।

 

সমাধানঃ

এখানে, (3+2k)x+5ky-3 = 0
⇒ 3x+2kx+5ky-3 = 0
⇒ 3x-3+k(2x+5y) = 0 ...(i)
(i) সমীকরণটি 3x-3=0 ⇒ x-1=0 ⇒ x=1 এবং 2x+5y=0 সরলরেখাদ্বয়ের ছেদবিন্দুগামী সকল রেখার জন্য সত্য ।
x=1 এবং 2x+5y=0 সমাধান করে পাই,
x=1, y=-2/5
∴ (1,-2/5) নির্ণেয় বিন্দু । [ans.]

 

6. (-1,2) বিন্দু দিয়ে যায় এবং 3x-y+7=0 রেখার সাথে 45° কোণ উৎপন্ন করে এরূপ রেখাদ্বয়ের সমীকরণ নির্ণয় কর ।

 

সমাধানঃ

 

এখানে, 3x-y+7=0 রেখার ঢাল = -(3/-1) = 3        [ax+by+c=0 রেখার ঢাল = -(a/b) ]
উক্ত রেখার সাথে 45° কোণ উৎপন্ন করে এরূপ সরলরেখার ঢাল m হলে,
tan 45° = ±(3-m)/(1+3m)
⇒ 1 = ± (3-m)/(1+3m)     

 

       

[দুইটি সরলরেখার ঢাল m₁ ও m₂ এবং তাদের মধ্যবর্তী কোণ θ হলে, $\tan \theta=\pm \frac{m_{1}-m_{2}}{1+m_{1} m_{2}}$]

‘+’ নিয়ে পাই, 3-m = 1+3m       ⇒ 4m = 2       ⇒ m = ½
‘-’ নিয়ে পাই, -3+m = 1+3m      ⇒ 2m = -4      ⇒ m = -2

∴ (-1,2) বিন্দুগামী m = ½ ঢালবিশিষ্ট সরলরেখার সমীকরণ,

y-2 = ½ (x+1)        [(x₁,y₁) বিন্দুগামী m ঢালবিশিষ্ট সরলরেখার সমীকরণ, y-y₁ = m(x-x₁)]
⇒ 2y-4 = x+1
⇒ x-2y+5 = 0     [ans.]
আবার, (-1,2) বিন্দুগামী m = -2 ঢালবিশিষ্ট সরলরেখার সমীকরণ,
y-2 = -2(x+1)
⇒ y-2 = -2x-2
⇒ 2x+y = 0     [ans.]

 

7. y অক্ষের সমান্তরাল এবং 2x-3y+4 = 0 ও 3x+3y-5 = 0 রেখা দুইটির ছেদবিন্দু দিয়ে যায় এরূপ সরলরেখার সমীকরণ নির্ণয় কর ।

 

সমাধানঃ

2x-3y+4 = 0
3x+3y-5 = 0
সমাধান করে, x = 1/5, y = 22/15           [use calculator to solve equations to save time]
∵ সরলরেখাটি y অক্ষের সমান্তরাল

∴ সরলরেখার সমীকরণ, x = 1/5
⇒ 5x-1 = 0     [ans.]

 

8. এমন একটি সরলরেখার সমীকরণ নির্ণয় কর যা 2x+3y+4 = 0 এবং 3x+4y-5 = 0 রেখা দুইটির ছেদবিন্দু দিয়ে যায় এবং 6x-7y+8 = 0 রেখার উপর লম্ব।

 

সমাধানঃ

2x+3y+4 = 0 ও 3x+4y-5 = 0 এর ছেদবিন্দুর স্থানাংক ≡ (-33,22) [use calculator]
∴ (-33,22) বিন্দুগামী 6x-7y+8 = 0 রেখার লম্ব রেখার সমীকরণ, -7(x+31)-6(y-22) = 0  

[(x₁,y₁) বিন্দুগামী ax+by+c = 0 রেখার লম্ব রেখার সমীকরণ, b(x-x₁)-a(y-y₁)=0]

⇒ -7x-217-6y+132 = 0
⇒ 7x+6y-85 = 0          [ans.]

 

9. (8,5), (-4,3) বিন্দু দুইটির সংযোজক রেখার লম্ব দ্বিখণ্ডকের সমীকরণ নির্ণয় কর ।

 

সমাধানঃ

উক্ত বিন্দুদ্বয়ের সংযোজক সরলরেখার ঢাল = (5-3)/(8+4) = 1/6      [ ঢাল = কোটিদ্বয়ের অন্তর / ভুজদ্বয়ের অন্তর ]
∴ উক্ত সরলরেখার লম্ব সরলরেখার ঢাল = $-\frac{1}{1 / 6}$   = -6     

[দুটি সরলরেখার ঢালের গুণফল -1 হলে তারা পরস্পর লম্ব]
(8,5),(-4,3) বিন্দুদ্বয়ের সংযোজক সরলরেখার মধ্যবিন্দু ≡ $\left(\frac{8-4}{2}, \frac{5+3}{2}\right) \mid$ ≡ (2,4)

[(x₁,y₁) ও (x₂,y₂) বিন্দুদ্বয়ের সংযোজক সরলরেখার মধ্যবিন্দু ≡ $\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)$ ]
∴ (2,4) বিন্দুগামী -6 ঢালবিশিষ্ট সরলরেখার সমীকরণ,

y-4 = -6(x-2)    [(x₁,y₁) বিন্দুগামী m ঢালবিশিষ্ট সরলরেখার সমীকরণ, y-y₁ = m(x-x₁)]
⇒ y-4 = -6x+12
⇒ 6x-y+26 = 0            [answer.]

 

10. এমন একটি সরলরেখার সমীকরণ নির্ণয় কর যার অক্ষ দুইটির মধ্যবর্তী খণ্ডিত অংশ (-4,3) বিন্দুতে 5:3 অনুপাতে অন্তর্বিভক্ত হয়।

 

সমাধানঃ

ধরি, সরলরেখাটির সমীকরণ, x/a+y/b = 1
অর্থাৎ সরলরেখাটি x অক্ষকে (a,0) ও y অক্ষকে (0,b) বিন্দুতে ছেদ করে।
∴ বিন্দুদ্বয়ের সংযোজক রেখা যে বিন্দুতে 5:3 অনুপাতে অন্তর্বিভক্ত হয় তার,

স্থানাংক ≡ $\left(\frac{5 \times 0+3 \times a}{5+3}, \frac{5 \times b+3 \times 0}{5+3}\right)$ ≡ (3a/8, 5b/8)

[(x₁,y₁) ও (x₂,y₂) বিন্দুদ্বয়ের সংযোজক সরলরেখা যে বিন্দুতে m₁:m₂ অনুপাতে অন্তর্বিভক্ত হয়, তার স্থানাংক ≡ $\left(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\right)$ ]

কিন্তু, 3a/8 = -4
⇒ a = -4(8/3)
⇒ a = -32/3
এবং, 5b/8 = 3
⇒ b = 3(8/5)
⇒ b = 24/3
∴ সরলরেখাটির সমীকরণ, $\frac{x}{-32 / 3}+\frac{y}{24 / 5}=1$
⇒ -3x/32 + 5y/24 = 1
⇒ 9x-20y = -96
⇒ 9x-20y+96 = 0      [answer.]

 

11. 12x-5y = 7 রেখার 2 একক দূরবর্তী সমান্তরাল রেখার সমীকরণ নির্ণয় কর ।

 

সমাধানঃ

12x-5y-7 = 0 রেখার সমান্তরাল কোন রেখার সমীকরণ, 12x-5y+c=0

প্রশ্নমতে, $\frac{|c+7|}{\sqrt{12^{2}+5^{2}}}=2$ = 2     

[ax+by+c₁=0 ও ax+by+c₂=0 সমান্তরাল রেখার মধ্যবর্তী দূরত্ব = $\frac{\left|c_{1}+c_{2}\right|}{\sqrt{a^{2}+b^{2}}}$ ]
⇒ ± (c+7) = 26
হয়, c+7 = 26                অথবা, -c-7 = 26
⇒ c = 19                              ⇒ c =-33
∴ নির্ণেয় রেখাংশ, 12x-5y+19 = 0  এবং 12x-5y-33 = 0

 

12. x-3y+2=0; x-6y+3=0; x+ay=0 রেখা তিনটি সমবিন্দু হলে a এর মান নির্ণয় কর ।

 

সমাধানঃ

∵ রেখাত্রয় সমবিন্দু  

                       ∴  $\left|\begin{array}{lll}1 & -3 & 2 \\ 1 & -6 & 3 \\ 1 & \text { a } & 0\end{array}\right|=0$

                       ⇒ $\left|\begin{array}{lcc}0 & 3 & -1 \\ 0 & -(\mathrm{a}+6) & 3 \\ 1 & \mathrm{a} & 0\end{array}\right|=0$   [r1´= r1-r2  ;  r2´= r2-r3]

                       ⇒ 9-(a+6) = 0
                       ∴ a = 3 [Answer.]

 

13. 4x+3y = c এবং 12x-5y = 2(c+3) রেখা দুইটি মূলবিন্দু থেকে সমদূরবর্তী । c এর ধনাত্মক মান নির্ণয় কর ।

 

সমাধানঃ

এখানে, 

$\frac{|4 \times 0+3 \times 0-c|}{\sqrt{4^{2}+3^{2}}}=\frac{|12 \times 0-5 \times 0-2(c+3)|}{\sqrt{12^{2}+5^{2}}}$
⇒ c/5 = 2(c+3)/13
⇒ 13c = 10c+30
⇒ c = 10          [Answer.]